合成速度と相対速度
エスカレーターや動く歩道の上を歩くと、階段や廊下を歩いているときよりも速く移動することができる。また、動いている複数の物体があるとき、1つの物体から別の物体を眺めると、相手は本来の速度とは異なった速度で動いているように見える。今回は、このような現象について考えていこう。
合成速度
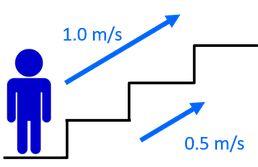
0.5m/sの速さで上るエスカレーターがある。このエスカレーターの上を1.0m/sの速さで歩いて上ると、上の階まで1.5m/sの速さで移動することができる。これは、
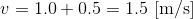
と計算した結果である。
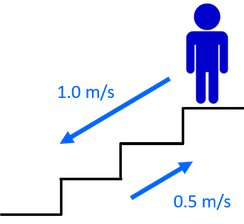
続いて、同じく0.5m/sの速さで上るエスカレーターを、今度は1.0m/sの速さで下る状況を考える。すると、下の階まで0.5m/sの速さで移動することになる。これは、
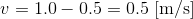
という計算の結果である。
ここで、速度は向きを持つ量だったことを思い出そう。上向きと下向きで逆向きだから、仮に上向きを正の向きとすると、人の速度は負の向きということになる。このことを考慮すると、上の計算は、
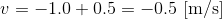
ということになる。計算結果が負ということは、負の向き、今は下向きを表している。
このようにして速度の和を考えることを「速度の合成」といい、計算結果を「合成速度」という。一般的に合成速度vは、元の速度をv1,v2として、
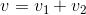
と表される。単純な公式だが、正の向きを決めて、負の向きの速度によく注意して足し算をするようにしよう。
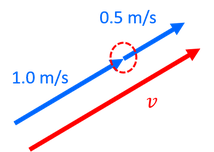
合成速度は、速度を矢印で表して考えることもできる。書き方は、まず1つ目の速度の矢印を描き、その終点から、2つ目の速度の矢印をつなげて描く。それができたら、1つ目の矢印の始点から2つ目の矢印の終点へ向かう矢印を描く。それが合成速度になっている。上のような図を書くことで、合成速度が上向きに1.5m/sであることが分かる。
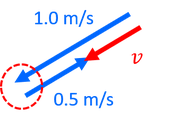
2つの速度の向きが逆の場合も、同様に図を書いて考えることができる。図より、合成速度が下向きに0.5m/sであうることが分かる。
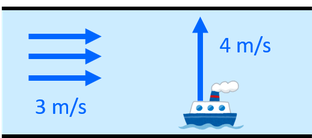
これまでは一直線上の運動ばかりを扱ってきたが、同じように考えると、平面上の運動を扱うこともできる。例えば、静水上ならば4m/sの速さで進むことができる船が、3m/sで流れる川を横切ろうとしている状況を考えてみる。
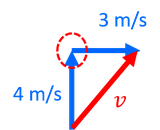
すると上のような直角三角形の図を書くことができるので、辺の比の関係から、合成速度の大きさが5m/sであることが分かる。
相対速度

東向きに20m/sで走る自動車Aから、東向きに30m/sで走る自動車Bを眺めると、東向きに10m/sで移動しているように見える。この「自動車Aから見た自動車Bの速度」のことを、「自動車Aに対する自動車の相対速度」という。この値は、

のように速度の引き算で求められることが分かる。
一般的に、「Aに対するBの相対速度」は、Aの速度v_Aと、Bの速度v_Bを使って、

と表される。

続いて、「自動車Bに対する自動車Aの相対速度」を考える。自動車Bから見ると、自動車Aは西向きに10m/sで進んでいるように見える。向きを考慮してこの相対速度を「-10m/s」と表すと、この値は、

と計算できることが分かる。
一般的に、「Bに対するAの相対速度」は、

と表される。
引き算なので、前後が入れ替わると答えが変わってしまうことが分かるだろう。ミスを防ぐためには、どちらが「自分」で、どちらが「相手」なのかを正確に読み取ることが大切だ。「Aに対するBの相対速度」であれば、自分がA、相手がBなので、「B-A」で計算できる。「Bに対するAの相対速度」なら自分がB、相手がAなので「A-B」で計算できる。「相手ー自分」と覚えておこう。
- 相対速度=相手の速度-自分の速度

相対速度は、速度の向きと大きさを踏まえた矢印を描くことによって求めることもできる。例えば「Aに対するBの相対速度」は、上図のようになる。書き方は、まず速度A、Bの矢印を「始点をそろえて書き」、自分(A)の矢印の終点から相手(B)の矢印の終点へ向かって新しい矢印を書けばいい。この図から、相対速度が「+10m/s」になっていることが分かる。

「Bに対するAの相対速度」も同じように考えることができる。今度は、自分がBで相手がAだから、Bの矢印の終点からAの矢印の終点へ向かって新しい矢印を書けばいい。この図から、相対速度が「-10m/s」になっていることが分かる。

(問) 西向きに20m/sで進む自動車Aと、東向きに30m/sで進む自動車Bがある。自動車Aに対する自動車Bの相対速度を求めよ。

(答) 東向きを正として、

よって、東向きに50m/s

これまでは一直線上の運動だけを考えてきたが、図によって相対速度が求められるようになると、一直線上以外の運動にも対応できるようになる。
いま、西向きに10m/sで進む自動車Aと、北向きに10m/sで進む自動車Bがあるとして、自動車Aに対する自動車Bの相対速度を求めてみよう。図を書くと、

上図のようになる。直角三角形になっているから、この辺の比を考えることで、Aに対するBの相対速度の大きさが分かる。

より

図から向きを読み取って、北東向きに14m/s。
