力と運動

合成速度と相対速度 ←→ 落体の運動

　速くなることを加速、遅くなることを減速という。このとき、どのくらい速度が変化するかの度合いを表す量を加速度という。今回はこの加速度について詳しく見ていこう。

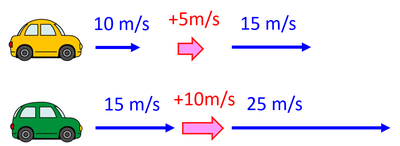
　10m/sで走っていた自動車の速度が同じ向きに15m/sになった場合と、15m/sで走っていた自動車の速度が同じ向きに25m/sになった場合を比較する。どちらの方が「より加速したか？」といえば後者だろう。理由は、「速度の変化量が大きい」からだ。

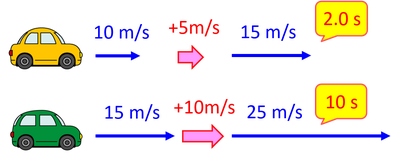
　では、前者の速度が5m/s増加するのに2.0秒間を要し、後者の速度が10m/s増加するのに10秒間を要したとしよう。するとどうだろう。「より加速した」という感じがするのは前者になる。理由は、加速に要した「時間が短い」からだ。

　このことを踏まえて、加速の度合いを定義しよう。速度の変化量Δｖ(m/s)が大きいほど、要した時間Δｔ(s)が短いほど大きくなるような量を考えてやればいい。

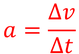
これを「加速度」という。〔m/s〕を〔s〕で割っているので、加速度の単位は〔m/s²〕となり、これをメートル毎秒毎秒と読む。この単位は「1秒間あたり何m/s速度が変化するか」を表していることが分かるだろうか。速さや速度と比較をすると、加速度は次のように定義することもできる。

• 加速度の定義…単位時間あたりの速度の変化量

　では、計算練習をしてみよう。例えば、2.0秒間で速度が5.0m/s変化したとき、その加速度は、 

となる。続いて、10秒間で速度が15m/sから25m/sに変化したとき、その加速度は、

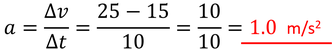
となる。速度の変化量Δｖの計算が「あと－まえ」になっていることに注意しよう。最後に、3.0秒間で速度が20m/sから5m/sに変化したとき、その加速度は、

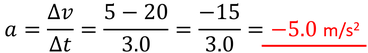
となる。負の値が出てきたのは、減速しているから。運動の向きを正の向きとすると、加速しているときの加速度は正の値で、減速しているときの加速度は負の値になる。覚えておこう。

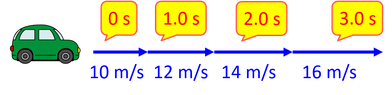
　一直線上を一定の加速度で進む運動を「等加速度直線運動」という。例えば10m/sで運動していた自動車の速度が、1秒ごとに12 m/s→14m/s→16m/s→…と変化していくとき、この自動車は一定の加速度2m/s²で等加速度直線運動をしているという。

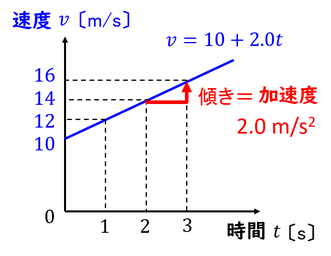
　この運動の様子をv-tグラフ上で表してみよう。すると、切片10，傾き2の一次関数となる。この関係を式で表せば、

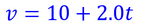
となる。切片10m/sはｔ＝０における速度、傾き2m/s²は加速度だから、これらをv_0，aとおけば、一般的に、等加速度直線運動をする物体の速度ｖと時間ｔの関係が、

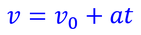
と表せることが分かる。ｖ_0を初速度という。

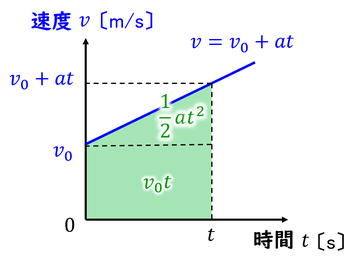
　また、等速直線運動ではv-tグラフの面積が移動距離を表していたことを思い出そう。実は、このことは等速直線運動以外にも成り立つのだ。そこで、等加速度直線運動のv-tグラフで囲まれた面積を計算することで、この運動における変位ｘと時間ｔの関係を知ることができる。

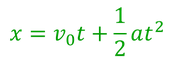
まとめ

• 等加速度直線運動の速度の式

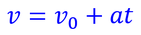
• 等加速度直線運動の変位の式

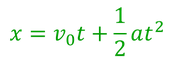
問題

　静止していた自動車が動きだし、一定の加速度4.0m/s²で速さを増している。この自動車が動き出してから3.0秒後の速度vと変位xを求めよ。

→まず速度vを求める。等加速度直線運動の速度の式より、

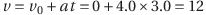
　よって、12m/s。

→次に変位xを求める。等加速度直線運動の変位の式より、

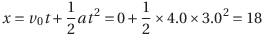
　よって、18m。