力のつり合い
力の分野に入り、力を矢印で表す方法と、作用反作用の法則や力のつり合いという力の関係の紹介をした。ただし、一直線上の力のつり合いしか考えていなかったので、今回はもう少し複雑な状況について考えてみよう。
重力
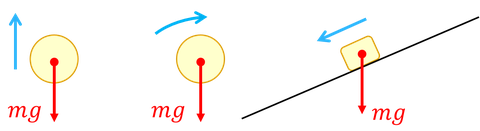
地球上の物体には「重力」がはたらいている。重力は「地球が物体を引く力」のことで、その大きさのことを「重さ」という。
重力を矢印で表す場合は、基本的には中心を作用点と考えて、そこから鉛直下向きに書くようにしよう。物体が静止していても、鉛直方向に運動していいても、斜めに運動していても重力は鉛直下向きなので、絶対に間違えないようにすること!
また、重さは力の大きさだから、単位は〔N〕である。日常的に体重が40kgだとか50kgだとか言っている量は、物理の用語としては実は重さではなく、「質量」と呼ばれる量である。
質量が大きな物体ほど重力も大きい。質量m〔kg〕の物体の重さW〔N〕は、mの約9.8倍になっていて、1kgの物体の重さは約9.8N,5kgの物体の重さは約49Nである。9.8というのは落体の運動のときに登場した量と同じく重力加速度だ。これをg〔m/s2〕とすると、重力の大きさは、
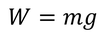
と表されることになる。重力の矢印を描いたら、その矢印が重力であることを強調して、近くにmgと書いておくとよいだろう。
張力
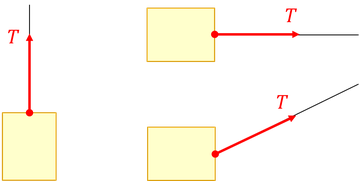
「糸が物体を引く力」を糸の「張力」という。張力は、物体と糸の接点が力の作用点で、「引く力」であることからも分かるように物体から離れる向きだ。張力は英語でTensionと書くので、Tという記号で表されることが多い。糸(String)ということで、たまにSも使われる。
垂直抗力
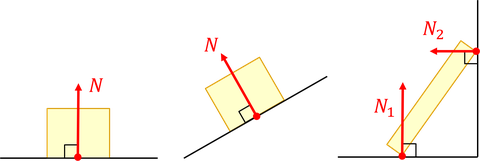
物体が机や床の上に置いてあるとき、物体は接触面から力を受けている。物体が、接触面から面に対して垂直な向きに受ける力を「垂直抗力」という。「面が物体を押す力」と表すことができ、力の作用点は面と物体との接点、向きは物体の内部へ向かう向きである。接触面は壁や斜面でもよいので、その場合の垂直抗力は水平方向や斜め向きになる。いつも鉛直上向きとは限らないので注意しよう。垂直抗力は英語でNormal Forceだから、Nという記号で表されることが多い。
摩擦力
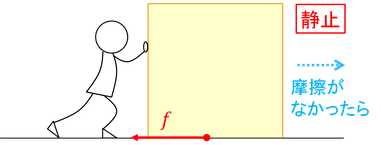
面から受ける力には、垂直抗力の他に「摩擦力」がある。摩擦力には2種類に分類でき、物体が静止しているときにはたらいているものを「静止摩擦力」、物体が運動しているときにはたらいているものを「動摩擦力」という。
静止摩擦力は物体が動こうとするのを妨げる向きなので、向きで悩んだら「摩擦がなければどちらに動くか」を考えて、その逆向きだと思えばいい。
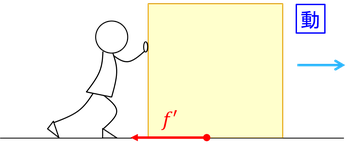
動摩擦力は、物体の運動を妨げる向きなので、動いている向きと逆向きだと思えばいい。
摩擦は英語でfrictionだから、摩擦力を表す記号にはFやfがよく使われる。静止摩擦力と動摩擦力を区別する場合は、動摩擦力をf'やF’とすることも多い。
弾性力
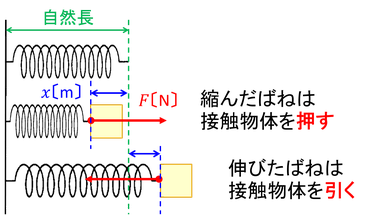
縮んだばねは伸びようとして接触物体を押し、伸びたばねは縮もうとして接触物体を引く。このように、変形したばねが元の長さに戻ろうとして接触物体に及ぼす力を、ばねの「弾性力」という。
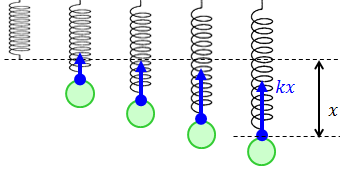

弾性力の大きさは、ばねの変形量(伸び・縮み)に比例して大きくなっていく。このきまりを「フックの法則」という。発見者のロバート・フックは、生物の分野でも細胞を発見した人として有名だ。フックの法則から、弾性力の大きさF〔N〕は、ばねの変形量をx〔m〕とすると、
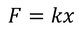
と表すことができる。k〔N/m〕はばねを1m変形させるのに必要な力の大きさであり、これを「ばね定数」という。ばね定数kが大きいほど固くて変形しにくいばねである。
力の合成・分解

あらい床の上の物体を押すと、その力以外に、物体には重力、垂直抗力、摩擦力がはたらく。ところで、床から受ける力が2種類あることに疑問を持った方はいらっしゃるだろうか。垂直抗力も摩擦力も、どちらも「床が物体を押す力」である。実は、床が物体を押す力は、図のように斜め向きの1つの力だけと見なすこともできるのだ。これを「抗力」と呼ぶ。
抗力と垂直抗力と摩擦力は、図のように、長方形の対角線と2辺という関係になっている。

一般に、2つの力と同じはたらきをする1つの力を「合力」と呼び、合力を求めることを「力の合成」と呼ぶ。抗力の例では長方形だったが、元の2力が直交していないときは平行四辺形となる。合力の求め方は、元の2力の矢印を2辺に持つような平行四辺形を書いて、その対角線を矢印に変えればいいことが分かる。

合成と逆の操作を考えることもできる。すなわち、抗力を垂直抗力と摩擦力の2つの力と考えてもよかったように、1つの力を、それと同じはたらきをする2つの力に分けて考えてもいいのだ。このような力をそれぞれ「分力」といい、分力を求めることを「力の分解」という。分力の求め方は、合成の逆なので、元の力の矢印を対角線に持つような平行四辺形を書いて、その2辺を矢印に変えればいい。
力の成分

力を分解する2方向はあらゆる角度に取ることができるが、今後絶対に身に着けてほしいのが、90度のときだ。分解を考える2方向が直交しているとき、平行四辺形は長方形になる。だから、元の力の矢印を対角線に持つような長方形を書いて、その2辺を矢印に変えるという操作をマスターして欲しいのだ。
ここで、各分力の方向にx軸、y軸を取る。このとき、x軸方向の分力を特に力の「x成分」、y軸方向の分力を力の「y成分」と呼ぶ。

今後、よく登場する角度を3種類挙げてみた。直角三角形の部分に注目して、30°,60°,90°の直角三角形の辺の比が1:2:√3であること、45°,45°,90°の直角三角形の辺の比が1:1:√2であることを利用して各成分の大きさを求めよう。できるかな?

また、角度がθであるとき、x成分の大きさはFcosθ, y成分の大きさはFsinθと表すことができる。これも覚えておこう。
力のつり合い

質量mのおもりをばね定数kのばねにつるすと、ばねはxだけ伸びて静止した。このように、いくつかの力がはたらいておもりが静止しているとき、おもりにはたらく「力がつり合っている」という。上下2つの力がつり合っているとき、この2つの力の大きさは等しい。このおもりには、上向きの弾性力F(=kx)と下向きの重力W(=mg)がはたらいているから、

という関係が成り立っていることになる。

床に置かれた質量m物体には、上向きの垂直抗力Nと下向きの重力mgという2つの力がはたらいている。だから、物体が静止していて力がつりあっているとき、

という関係式が成り立っている。

あらい床の上にある物体の右側に糸を付けて引くと、物体には重力mg,垂直抗力Nの他に糸の張力Tと摩擦力fがはたらく。物体が静止している場合、この4つの力はつり合っていると言える。このときは、上向きの力と下向きの力の大きさが等しくなっていることに加えて、左向きの力と上向きの力の大きさが等しくなっている。

物体が静止するためには、この両方が成り立っている必要がある。例えば「N=mg」だけだと、右や左に動き出す可能性がある。

これで、上下左右の4つの向きに力がはたらいて物体が静止しているとき、「上=下」「左=右」という2種類のつり合いの関係式が作れることが分かってもらえたと思う。では、斜め向きの力がある場合はどのように考えたらよいのだろう。

前回、1つの力と同じはたらきを持つ2つの力を求める作業を紹介した。力の分解だ。斜め向きの力がある倍は、この力を分解して、上下・左右方向の2方向の力の成分を取り出すことで、力のつり合いの関係式を考えることができるのだ。

例えば図のような状況では、張力Tを上向きの成分Tsinθと右向きの成分Tcosθに分けることができるから、これらを用いて

という2種類の力のつり合いの関係式を表すことができる。
力のつり合いの問題では、
- 斜めの力は分解する!
ということを合言葉にして考えるようにしよう。

もう少し問題を解いてみよう。
天井から糸でつるされた10Nのおもりを、水平右向きに大きさFの力で引く。天井と糸の間の角度が30°になったとき、Fと、張力の大きさTはいくらだろうか。

鉛直方向(上下方向)、水平方向(左右方向)の力のつり合いの式を立てるために、斜め向きの張力Tを分解して成分を考えよう。図を書いて考えると、上向きはT/2, 左向きは√3T/2であることがわかる。このことから、

という2種類の力のつり合いの式が作れるので、この2式を解くことで、

TとFが求められる。

実は、分解して力のつり合いの関係を考える2方向は、鉛直&水平でなくても構わない。例えば、おもりをつるした2本の糸が90°になっている場合、

このように、2本張力を分解して、鉛直方向と水平方向の力のつり合いの式を考えてもよいが、

重力を、2本の糸と同じ方向に分解してもよい。すると、直交する2本の糸と同じ方向の力のつり合いの式は、

となる。なんと、この式を立てると同時に張力T1,T2が求められてしまうのだ。
力のつり合いを考える2方向は直交していればいい。だから、力の矢印を書いて、直交している2つの力がある場合は、その力の2方向について力のつり合いを考えるとよい。

あらい斜面に乗って静止した物体にはたらく力は、重力mg,垂直抗力N,摩擦力fの3つである。垂直抗力Nと摩擦力fが直交しているから、斜面方向と斜面に垂直な方向について力のつり合いを考えるといい。

斜面方向と斜面に垂直な方向の力のつり合いを考えるためには、重力mgを分解する必要がある。角度θの位置に注意すると、斜面方向の成分の大きさがmgsinθ, 斜面に垂直な方向の成分の大きさがmgcosθになるから、力のつり合いの2式は、

となる。垂直抗力の大きさNと摩擦力の大きさfを求める問題だったら、力のつり合いの2式を立てたと同時に求められる。
