力と運動

慣性モーメント ←

　力のモーメントの和が0でないとき，剛体は回転運動を始める。今回は，剛体の振り子である実体振り子と，コマやヨーヨーの運動について詳しく見ていこう。

　任意の点Oを通る回転軸gのまわりの慣性モーメントIを求めてみよう。重心Gを通り，回転軸gに平行で距離hだけ離れた回転軸g'のまわりの慣性モーメントをI_Gとする。また，O点を原点に持つx軸と，G点を原点に持つx'軸を考え，棒をN個に分割すると，i番目の位置xiからO点までの長さは

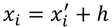
である。この位置の部分の質量をm_iとすると，O点のまわりの慣性モーメントは

と表される。棒全体の慣性モーメントIは，これを分割された部分すべてで足し合わせればいい。

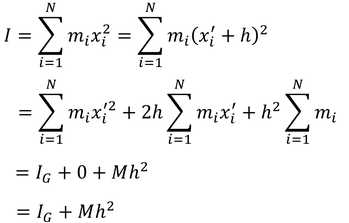
この関係が成り立つことを，平行軸の定理と呼ぶ。

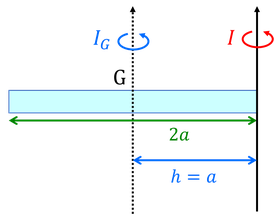
　例えば，長さ2aの棒の端のまわりの慣性モーメントIは，重心Gのまわりの慣性モーメント

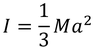
および平行軸の定理より

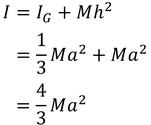
と求められる。

　剛体の1点を固定して回転軸とした実体振り子の周期を求めよう。剛体の質量をM，回転軸と重心の距離をhとし，回転角θの瞬間について，回転運動の運動方程式（Iα＝N）を立てると

となる。ただし，回転角θは非常に小さいものとした。これにより，回転運動の角加速度

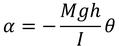
を得る。このことから，角振動数

および振動の周期

を得る。ここで

とおくと，周期は

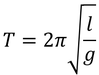
このように単振り子と同じ式になる。lを，相当単振り子の長さと呼ぶ。また，平行軸の定理

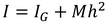
を用いると、単位相当振り子の長さを

と表すこともできるが，相加相乗平均の大小関係より

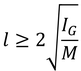
単位相当振り子の長さの最小値を得る。このことから，周期の最小値

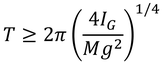
を得ることもできる。周期が最小値になるのは，相加相乗平均の等号成立の条件より

のときだと分かる。

　コマを回すと，回転数の大きな初めのうちは回転軸が直立しているが，徐々に回転数が減少していくと，回転軸が円錐を描くようにふらふらと回転を始める。コマの回転軸のまわりの角速度をωとし，回転軸の角速度Ωを求めてみよう。角運動量と力のモーメントの関係を用いる。

回転軸の鉛直からの角度をθ，コマの重心から回転軸に沿って床までの長さをｌとすると，重力Ｍｇによる力のモーメントの大きさＮは

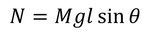
である。また，コマの回転の角運動量の向きは回転軸に沿う向きで，その大きさLは

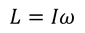
である。ここで，角運動量ベクトルの変化量は，中心角dφを用いて

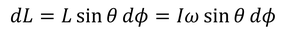
と表されるから，角運動量と力のモーメントの関係は

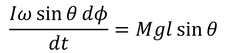
となる。よって，回転軸の角速度Ωが

こうして得られる。

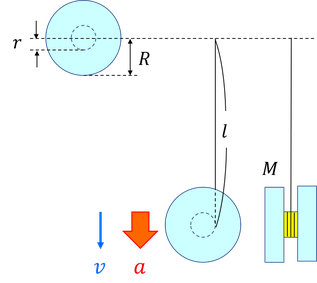
　質量の無視できる半径ｒの円柱に糸を巻き付け，その円柱を半径Ｒの2枚の円板ではさんだヨーヨーの運動を考える。手をはなすと，ヨーヨーが回転して糸が伸びていく。糸の長さがｌになった瞬間の，ヨーヨーの重心の速さｖと加速度の大きさaを求めよう。

　速さｖを求めるには，力学的エネルギー保存則を用いるとよい。ヨーヨーの運動エネルギーは，重心の運動エネルギーと，重心のまわりの運動エネルギーに分離して考えることができる。重心のまわりの運動エネルギーは，質量mの各部分の運動エネルギーの和を考えるとよい。

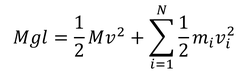
右辺第2項（重心のまわりの運動エネルギー）は

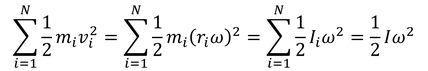
と表されるので、力学的エネルギー保存則の式は

となる。さらに，円板の慣性モーメントが

であることと

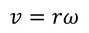
の関係を用いることで

速さｖを得る。

　加速度の大きさaを求めるためには，糸の張力をTとして，運動方程式

および回転運動の運動方程式

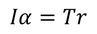
の2式を

の下で解けばよい。