連続固有値
前回は演算子がとびとびの固有値を持つ場合を考えたが、演算子が連続的な固有値を持つ場合もある。次は、そのような場合を考えてみよう。代表的なものには、座標xや運動量pがある。
連続固有値
演算子Aが連続的な固有値aを持つとき、固有値方程式は次のように表される。
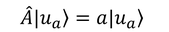
この固有ベクトルの正規直交条件は、固有値がとびとびになるときの固有ベクトルの正規直交条件の式に現れたクロネッカーのデルタをデルタ関数に置き換えて、
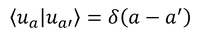
と表される。また、完全性の条件は、∑記号を積分記号に書き変えて
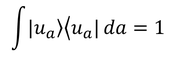
と表される。
連続的な固有値を持つ演算子には、座標xや運動量pがある。では、座標や運動量を基底ベクトルとして、ほかの物理量を表すことを考えてみよう。座標を用いて表す方法を座標表示、運動量を用いて表す方法を運動量表示と呼ぶ。例えば、運動量を座標で表示するとは、
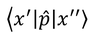
を求めることである。演算子を行列で表したときにその成分を求める式と比べるといい。では求めてみよう。演算子xに対して左側からブラを与えたとき

こうして固有値が取り出せることと、デルタ関数の公式
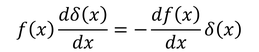
を用いて、座標xと運動量pの交換関係

をx'のブラとx''のケットではさんで計算すると、

および
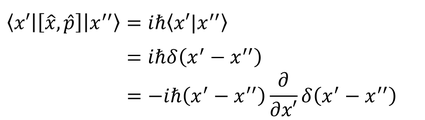
を得るので、2式を比較することで

こうして運動量の座標表示が求められる。
同様に、p'のブラとp''のケットでxとpの交換関係を挟んで計算すると、
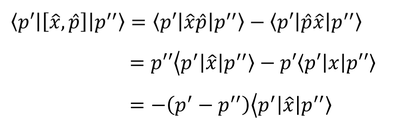
および
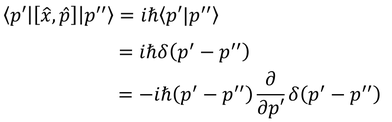
を得るので、2式を比較することで、

こうして、座標xの運動量表示が求められる。
基底の変換
次は、運動量pを用いた基底ベクトル|p〉と、座標xを用いた基底ベクトル|x〉の間にある関係を求めてみよう。|x〉の完全性の条件
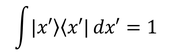
を用いて次のを計算すると
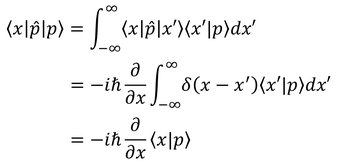
となるが、
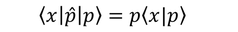
でもあるから、
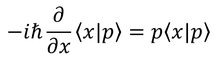
を得る。これを解くと、xの状態ベクトルとpの状態ベクトル内積が

こうして求められる。積分定数Cは、
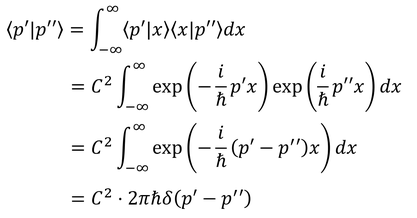
と正規直交条件
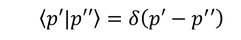
を用いて得られる。
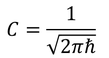
こうして得られた
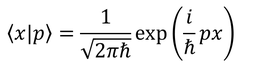
を用いることで、pで表した基底ベクトルとxで表した基底ベクトルの間の関係

が得られる。状態ベクトル|p〉の正規直交条件を利用してこれを求めたが、
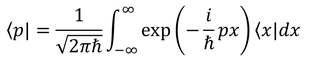
を用いて、|p〉が完全性を示すことも

こうして示すことができるので、|p〉が基底であることが分かる。
ハイゼンベルクの運動方程式
話題を少し変えよう。シュレーディンガー方程式

の波動関数を状態ベクトルの形で表すと、
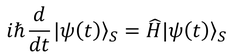
となる。これを解くと

となる。ここで、時刻t0における波動関数を

と書くと積分定数Cが

と求められるので、波動関数が決まる。
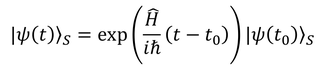
気を付けて欲しいのは、波動関数Ψ(t)は時間の関数だが、演算子Hは時間変化する量ではないということ。このような状態の表し方を、シュレーディンガー描像と呼ぶ。
一方、ある物理量Aの期待値は

と表されるわけだが、この式は時間変化しない波動関数の部分(青色)と、時間変化する演算子の部分(赤色)に分類することができる。このように、波動関数は時間変化する量ではなく、演算子が時間変化すると考える状態の表し方を、ハイゼンベルク描像と呼ぶ。また、演算子A(t)を時間微分すると
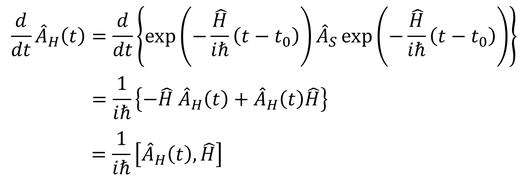
となり、こうして得られる
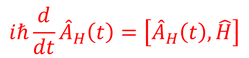
この式を、ハイゼンベルクの運動方程式と呼ぶ。シュレーディンガー描像における運動方程式がシュレーディンガー方程式、ハイゼンベルク描像における運動方程式がこの式というわけだ。
