軌道角運動量
ここまで3回に分けて水素原子のシュレーディンガー方程式を解いてきた。電子は原子核の周りに雲のようにぼんやりと存在しており、回転しているわけではないということを話してきたが、実は角運動量を考えることができる。今回はそれを紹介しよう。
角運動量
前回、新しく

という波動関数を導入した。これをr方向のシュレーディンガー方程式

に適用しよう。R=χ/rの微分が
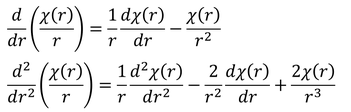
だから、
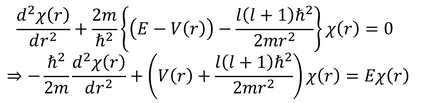
となる。この式は、1次元ポテンシャルを考えた場合の、時間に依存しないシュレーディンガー方程式と似た形になっている。唯一異なるのは、ポテンシャルの項に
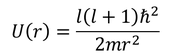
が追加されているという点だ。これは何だろう。

ここまでに考えてきたポテンシャルV(r)は静電気力によるものだった。見方を変えれば、電子は遠心力を受けていると見なすことができるから、U(r)は遠心力によるポテンシャルであると考えることができる。遠心力fは、円の半径r,電子の速度vを使って
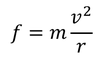
と書ける。ただし、実際に周回運動しているわけではない電子の速度vを考えるわけにはいかないので、消去したい。そこで、円運動をする物体の角運動量

を用いてvを消去する。すると、

となる。また、ポテンシャルU(r)をrで微分することで、

このように、遠心力fを得ることもできる。2式を比較することで、この角運動量Lを、軌道各量子数lで表すこともできる。

角運動量演算子

一般的に角運動量Lは、位置ベクトルrと運動量ベクトルpの外積で表されるベクトルである。
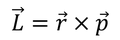
しかし、量子力学では位置と運動量はどちらも演算子なので、角運動量も演算子であると言える。書き出してみると、

となる。ベクトルを太字で表すことがあるのでそうしてみた。ここで、x,y,z成分をそれぞれ極座標で表してみる。3次元極座標のラプラシアンを導出したときを思い出そう。


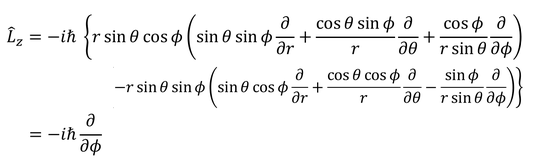
さらに、それぞれ2乗して

足し合わせると、

演算子L^2が得られる。
この結果をY(θ,φ)に作用させると、

となるが、ここで

という関係を思い出せば、
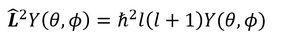
を得る。これは固有値方程式になっている。この式からも、角運動量の大きさが

であることが分かる。
角運動量に関する固有値方程式はほかにも考えられる。例えば、角運動量のz成分をΦ(φ)に作用させると、

となり、z成分の固有値が得られる。

角運動量の不確定性関係
角運動量の各成分どうしの交換関係を求めてみよう。x成分とy成分の交換子を考えて計算してみると、

のようになる。ここで、

より、
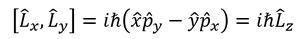
を得る。同様に、

等関係も導出できる。これらの結果が0ではないということから、角運動量の各成分は、同時に確定しないということが分かる。

そこで、見方を変えて、L^2とL_zの関係を見てみよう。交換子を計算してみると、

となる。ここで、
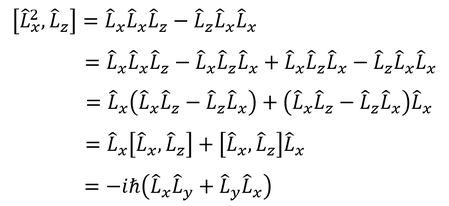
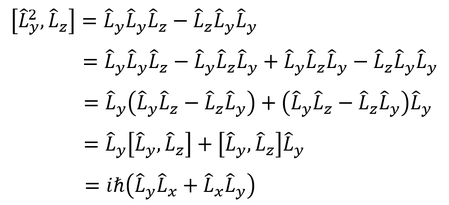
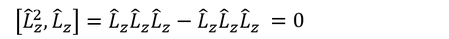
より、
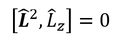
を得る。交換子が0ということは、この2種類の演算子の間には不確定性関係がないということだ。L^2の固有値から、角運動量の大きさ|L|が分かる。つまり、|L|とLzは同時に確定するということなのだ。

では、角運動量とその成分の間の関係を考えてみよう。
① l=0,m=0のとき

となる。これはつまり、s軌道のときは角運動量がないということを表している。
② l=1,m=0のとき
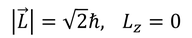
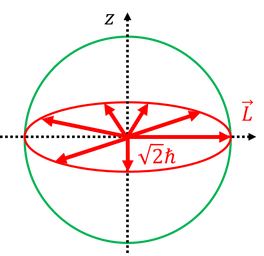
このときは、図のようにxy平面上のベクトルになる。ただしz成分が確定しているということは、不確定性関係からx成分とy成分はまったく確定していないことになるので、円周上のどこかにあるというわけではなく、ぼんやりと広がって分布している。
③ l=1,m=+1のとき

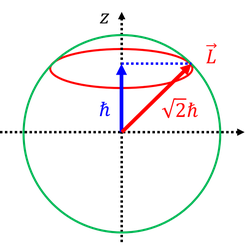
このように、z軸正の向きにz成分を持つような、大きさ√2hバーの角運動量ベクトルになる。ただし、x成分とy成分はまったく確定しないので、円周上にぼんやりと広がる。
④ l=1,m=-1のとき


となる。このように、角運動量はとびとびの値しか取らないということに注目しておこう。

ところで、主量子数nと軌道量子数lが等しく、mだけが異なる状態で縮退している原子があるとする。縮退している場合エネルギーが等しいが、磁場を加えると、そのエネルギー準位が分裂する。すると、原子から放出される電磁波の波長は、もともと1種類のみであるが、複数の波長が放出されるようになる。すると、スペクトル線が磁場を加えることで複数に分裂して現れる。この現象を「ゼーマン効果」という。ゼーマン効果には正常ゼーマン効果と、異常ゼーマン効果があり、この現象は正常ゼーマン効果である。
