無限の井戸
ミクロな粒子の存在確率は波動関数によって表され、観測によって1つに定まる。物理量の演算子はいくつかの固有値を持ち、対応する波動関数を固有関数という。今回はシュレーディンガー方程式を解き、固有値と固有関数を求めてみよう。
固有値方程式
固有値と固有関数を求める方程式を「固有値方程式」という。
時間に依存しないシュレーディンガー方程式
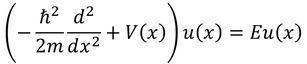
も固有値方程式になっており、これを解くことでエネルギー固有値Eと、それに対応する固有関数u(x)を求めることができる。
u(x)の意味について考えてみる。元のシュレーディンガー方程式の解である波動関数Ψ(x,t)がxの部分とtの部分に分けられるとき、

と書くことができた。この式を使うと、波動関数の規格化条件は
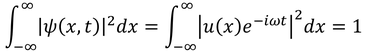
となるが、f(t)の2乗が

となることから、規格化条件は、
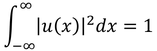
となる。つまり元の波動関数Ψ(x,t)の確率要素は、u(x)だったことが分かる。
井戸型ポテンシャル

x=ーa~aのポテンシャルが0で、それ以外のポテンシャルが無限大になっているような空間を考えよう。非常に強い引力で中心んに引き付けられており、決してこの範囲から抜け出せないことを意味している。この”井戸”の内部に粒子があるとき、古典的な粒子であれば、範囲内を往復するだけであるが、量子力学的な効果を考えると、粒子はどのようなふるまいをするのだろうか。
とりあえず井戸の外はポテンシャルが無限大だから、粒子は存在できないはずだ。そこで、井戸の外において波動関数u(x)=0としておく。
続いて井戸の内部について考える。この内部で粒子が定常波を作っているとすれば、波動関数はxの部分とtの部分に分けられるから、時間に依存しないシュレーディンガー方程式

を解いていく。この式は

となるので、ここで

とおくと

となるから、一般解
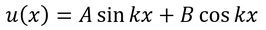
を得る(A,Bは定数)。
定数A,Bを求めるためにはどうするか。そのために、井戸の外では波動関数がu=0だったから、井戸の内外でこれをつなげるために、x=±aにおいてu=0という境界条件を導入しよう。
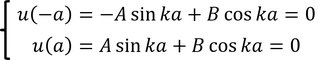
これらより、

が得られる。これらが成り立つためにはA=0,B=0であればよいが、その両方が0のとき、波動関数u(x)がxによらず常に0となってしまい、粒子が存在しないことになってしまう。そのため、両方が0になってはいけない。そこで、場合分けをして考える。
①A=0(B≠0)のとき

だから、波動関数は

となる。定数Bは規格化条件から、

よって、

②B=0(A≠0)のとき

よって、波動関数は
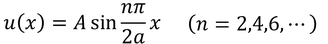
となる。定数Aは規格化条件から、

よって、

エネルギー固有値
固有関数u(x)が求められたので、次は対応するエネルギー固有値Eを求めよう。kの値から

これらより

と求められる。では、いくつか固有関数u(x)とエネルギー固有値Eを並べてみよう。
①n=1のとき
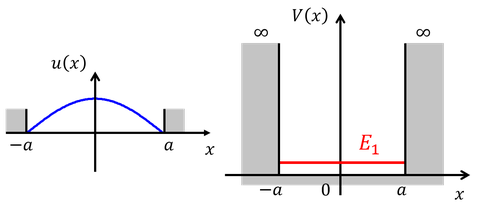
②n=2のとき

③n=3のとき
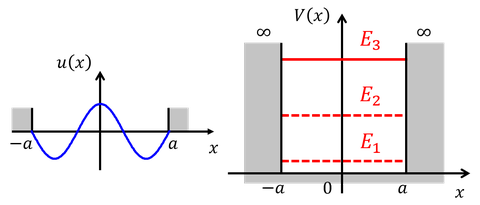
nが奇数の時はコサイン関数、偶数の時はサイン関数となる。また、エネルギー固有値は、n^2に比例して1,4,9,…と大きくなっていく。
エネルギーが最小になるのはn=1のとき。古典的な粒子であれば、静止するとエネルギーが0となってこれが最小値となるが、量子力学の効果を考えると0にはならない。

これを「零点エネルギー」という。
