光の運動量
アインシュタインは、光電効果の結果などから、光はエネルギー

を持つ光子の集まりであると考えた(c=νλ)。この考えを「光量子仮説」という。また、粒子であれば運動量を持つだろうと考え、これを
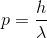
とした。
コンプトン効果
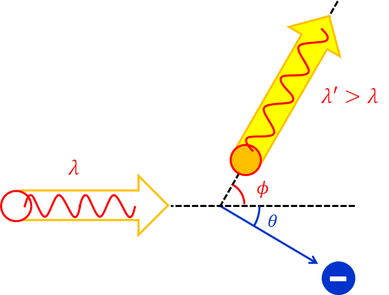
X線を物質に照射すると、いろいろな方向に散乱される。その散乱波には、もとの波長と同じものと、それよりも長い波長のものが含まれる。この現象を「コンプトン効果」という。X線が波として物質内の電子を振動させたとすれば、その振動の振動数はX線の振動数と等しくなるはずであり、その結果として放出されるX線の波長は元のものと等しくなるはずである。
この問題を解決するため、X線をエネルギーと運動量を持つ光子として考え、このX線光子が物質内の電子に衝突し、弾き飛ばしていると考えてみよう。すると、電子を弾き飛ばすことに光子はエネルギーの一部を失い、X線の波長は伸びるはずだ。このことを証明してみたい。まず、エネルギー保存則より、

続いて、運動量保存則より、
x方向
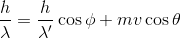
y方向
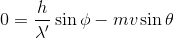
この3式から、電子の散乱角θと、速度vを消去する。先に運動量保存則の式を用いてθを消去しよう。

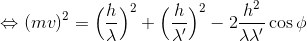
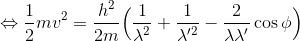
続いてこれをエネルギー保存則の式へ代入してvを消去する。


ここで、λ'≒λとすれば

だから、波長の伸びΔλ(=λ'ーλ)が計算できる。

この結果が、実験と一致していたことから、光子が「h/λ」という運動量を持つことが確かめられた。
光子気体の運動量
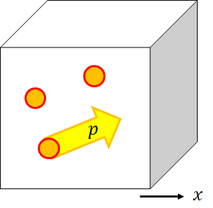
では光子の運動量を導出してみよう。色々な導出方法があるが、今回は光子気体の運動を考えることにする。1辺Lの立方体に、N個の光子が閉じ込められている。ここで、1個の光子の速さをc、運動量をpとすると、x方向の運動量は
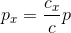
となるから、この1個の光子は内壁から、大きさ
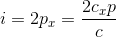
の力積を受け取ることになる。この光子は、同じ内壁に1秒間で

回衝突するので、1秒間あたり、

の力積を受けていることが分かる。これは、力積の定義から、光子が受ける平均の力と一致する。ここから、N個の光子全体が内壁から受ける力が求められる。
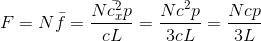
途中で、光子の速さcは一定であるから、

とした。これで、光子が内壁に与える圧力が求められる。
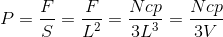
体積をV(=L^3)とした。
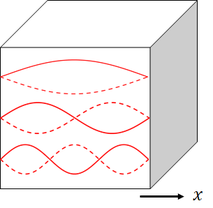
続いて、光が定常波になっているとして、その振動数を求めよう。これは、以前「プランクの法則」のところで説明したように、

となる。ここから、容器をゆっくりと断熱膨張させ、一辺がL+ΔLの立方体になったとする。このとき、定常波の形が変わっていなければ、その振動数の変化は、

となる。ここで、分母にL+ΔL≒Lを用いると、

となる。また、体積変化が
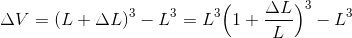
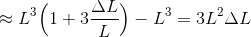
だから、これを用いることで、Δνは

となる。
N個の光子のエネルギーの和は「E=Nhν」であり、容器の体積を断熱膨張させたときの光子がした仕事は「W=PΔV」だから、熱力学第1法則より、

が成立する。ここへ先に求めた値を代入してまとめると、

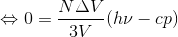
よって、

これで、光子の運動量が導けた。
