ボーアの理論
電子が発見され、原子にも構造があることが次第に分かってきたころ、原子の大きさと構造を調べるさまざまな研究が行われ、いくつかの原子モデルが考えられた。
ラザフォードの太陽系モデル

原子の大きさを調べるため、ガイガーとマースデンはラザフォードの指導の下、α線を金箔に照射する実験を行った。彼らが想定していた原子モデルはJ.J.トムソンが考えた「ブドウパンモデル」であり、原子の縁で大きな静電気力を受けて曲げられるため、原子の大きさが分かるはずだった。
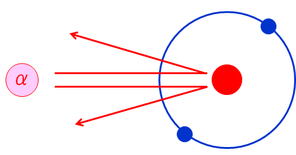
ところが結果の中に、ごくわずかな量ではあるが、90°以上の大きな角度で散乱されたものがあった。これは、非常に小さな領域に、正電荷が集まっていることを示唆していた。これが今でいう「原子核」である。ラザフォードはこの結果から、原子核の周りを電子が回っている「太陽系モデル」を考え出した。
ラザフォードモデルの問題点

ラザフォードのモデルでは説明ができない現象が観測された。水素などの気体が放つ電磁波の波長が、連続的ではなくとびとびだったのだ。水素原子については、可視光線領域をバルマーが、紫外線領域をライマンが、赤外線領域をパッシェンがそれぞれまとめ、結果的に次のような式で波長が表されることが分かった。

R(≒1.1×10^7/m)を「リュードベリ定数」という。
もう一つ、ラザフォードのモデルでは説明ができない現象があった。もし、電子が原子核の周りを円運動をしているのならば、電子は電荷をもっているため、その回転に応じた振動数の電磁波を放出してエネルギーを失ってしまうはずなのだ。そして、エネルギーを失った電子は原子核へと落下していくことになる。しかし、もちろん現実としてそのようなことは起きていない。
ボーアの原子モデル

以上の問題を解決するモデルとして、ボーアは以下の2点を仮定した。
- 電子は、角運動量mvrがh/2πの整数倍となるような軌道に存在している限りは安定である。
- 電子はそれぞれの軌道を移動することができ、その差を持つエネルギーhνの光子が放出または吸収される。
1つめの仮定を「ボーアの量子条件」、2つめの仮定を「ボーアの振動数条件」という。
量子条件は、

と表すことができる。「h/2π」は今後よく出てくるので、hバーという記号で表すことも多い。
振動数条件は、

と表すことができる。
この2つの仮定から、実験結果である水素原子のスペクトルを表す式を理論的に導くことで、2つの仮定が正しいことを確かめてみよう。まず、電子の運動方程式

に量子条件を代入することで、電子の速さvを消去する。
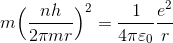
ここから、電子の軌道半径rを求めることができる。
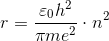
n(=1,2,3,…)を「主量子数」という。このことから、電子の軌道がとびとびになっていることが分かる。水素原子について、n=1のときの半径を「ボーア半径」といい、約0.5×10^(-10)mである。ここから、原子の大きさ(直径)が約10^(-10)mであることが分かる。
また、電子がそれぞれの軌道に収まっている状態を「定常状態」、定常状態における電子が取ることができるエネルギーを「エネルギー準位」という。さらに、n=1のときを「基底状態」、n>2のときを「励起状態」という。
続いて電子が持つエネルギーは、

なので、ここへ円運動の運動方程式を思い出せば、

となる。さらに、軌道半径rを代入することで、

となる。よって、エネルギー準位の大きさは、主量子数nの2乗に反比例してとびとびに変化していることが分かる。
最後に、このエネルギーの式を振動数条件へ用いることで、
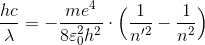
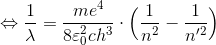
ここで、

とすれば、

水素原子のスペクトルを表す式になる。このRは実際のリュードベリ定数を同じ値であり、このことから、ボーアの2つの仮定は正しいということが分かった。
では、どうして電子はとびとびの軌道にしかいることができないのだろうか。ボーアがこの答えにたどり着くのは、ここから11年の年月が必要になる。
