シュテファン・ボルツマンの法則
前回はプランクの法則の導出をしたが、今回はプランクの法則を使って、それ以前に知られていた黒体放射に関する法則の導出をしてみたいと思う。
シュテファン・ボルツマンの法則
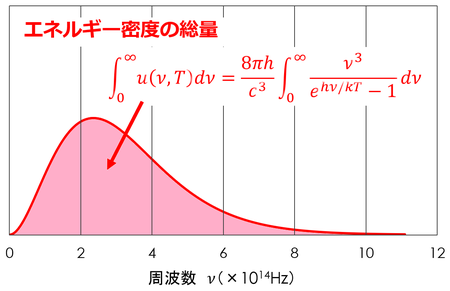
エネルギー密度u(ν,T)をすべての周波数で積分する。

これはエネルギー密度の総量を表している。ここで、

とおき、公式

を用いることで、
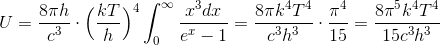

が得られる。これはシュテファン・ボルツマンの法則である。
ウィーンの変位則

エネルギー密度u(ν,T)をu(λ,T)に変換することを考える。周波数ν~ν+dνのエネルギー密度

これを、

を用いて変形する。ただし、正の値しか考えないので、マイナスの符号は考えなくてよい。
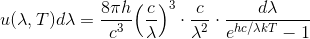
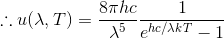
続いて、この式の微分が0となる条件を考える。
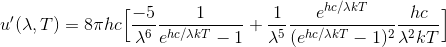

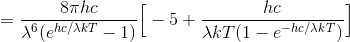
これが0になるためには、前半部分か、後半の[ ]が0になればよい。前半部分が0となるのはλ→∞の場合である。[ ]が0となるのはグラフのピーク部分である。[ ]の中身について、

とおき、
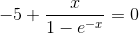
を解くことを考えてみよう。簡単には解けないが、グラフを書いて、横軸と交わる点を読み取ればxが決まる。
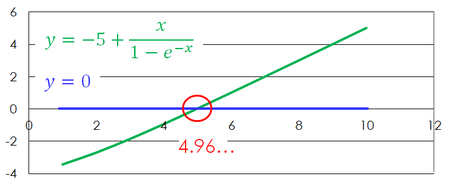
だいたい5である。大切なのは、xが1つに決まるということで、つまりxは定数であるということ。これにより、グラフのピーク部分の波長が、
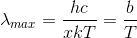
と求められる。これは、ウィーンの変位則である。
ウィーンの放射法則とレイリー・ジーンズの法則
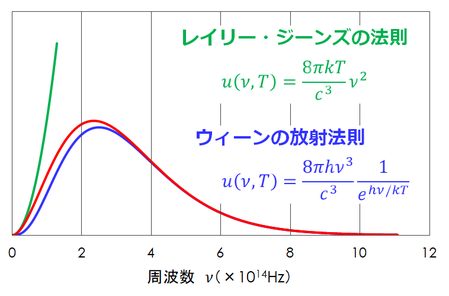
周波数が大きいとき、ウィーンの放射法則はプランクの法則とよく一致する。周波数が小さいとき、レイリー・ジーンズの法則はプランクの法則とよく一致する。
いま、周波数νが非常に大きいとすると、
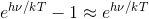
だから、プランクの法則を
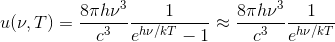
と書き変えることができる。これは、ウィーンの放射法則である。
続いて、周波数が0に近いとき、
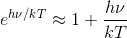
だから、これをプランクの法則に用いると
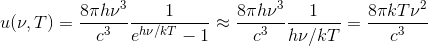
が得られる。これは、レイリー・ジーンズの法則である。
