エルミート演算子
位置と運動量の間には不確定性関係があることを学んだ。今回はこの関係をほかの物理量にも拡張し、演算子や物理量の一般的性質について考えてみよう。
エルミート共役
期待値の計算をするとき、演算子を、波動関数の複素共役と、元の波動関数ではさんで表した。いま、この波動関数を1,2と区別したとき、演算子Aは後ろ側の2番に作用していることになる。もし別の演算子Bを用意して、これを1番に作用させようと思ったら、1番の前に持ってこなければならない。この2つの式が等しくなるとき、演算子Bを、演算子Aの「エルミート共役」と呼び、これを「A†」と表す。

1番2番を区別せずに、
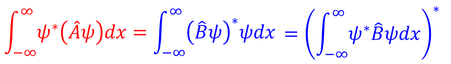
と定義されることもある。場合に応じて使い分ければいい。また、演算子Aと演算子B(=A†)が等しいとき、演算子Aを「エルミート演算子」という。
例えば運動量演算子について、次のような式を変形していくと、

このように、エルミート演算子の定義通りになる。このことから、運動量演算子はエルミート演算子であることがわかる。一般的に、物理量を表す演算子はエルミート演算子である。
固有値
物理量の偏差ΔAの演算子を次のように定義し、これが0であるとする。
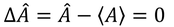
このような関係を満たすような波動関数Ψ_0があるとき、
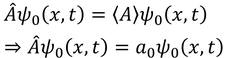
Ψ_0を「固有関数」といい、1つに定まった値a_0を「固有値」という。固有値が複数あるとき、それぞれの固有値に対応した固有関数が存在している。
では、固有値と固有関数の性質をそれぞれ見ていこう。まずは固有値の性質から。Aをエルミート演算子とすると、次のような式が成り立つ。
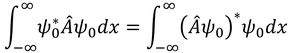
両辺を固有値で書き変えると、
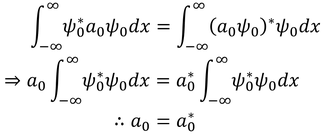
となる。このことから、エルミート演算子の固有値は実数であるということが分かる。
続いて、エルミート演算子Aについて、次のような2組の固有値と固有関数があり、
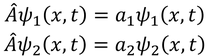
a_1≠a_2であるとする。エルミート演算子の定義より、

となる。この関係を持つΨ_1とΨ_2を、直交しているという。一般に、複数の固有値に対応するそれぞれの固有関数は直交している。
直交する固有関数を多数用いると、任意の波動関数が固有関数の重ね合わせで表現できる。
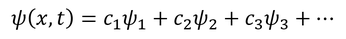
もともと波動関数はたくさんの固有関数が重なり合っていて、観測によってそのうち1つが選び出されると考えれば、実験事実と適合する。この式の係数c1,c2,…は、それぞれの固有関数が現れる確率に対応している。
交換関係
位置xと運動量pの積を、波動関数Ψに作用させると、
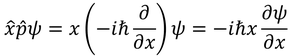
となる。運動量pと位置xの積を、波動関数Ψに作用させると

となる。このことから、xとpの積は、順番によって結果が変わってしまうことが分かる。このような関係を「非可換」、積の順番を入れ替えても結果が変わらない関係を「可換」という。この関係は交換関係と呼ばれ、これらは
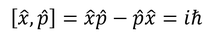
という、交換子を用いて表現することもできる。交換子が0であれば可換、0でなければ非可換というわけだ。
この交換関係から、物理量A,Bの不確定性関係を導出することもできる。いま、エルミート演算子A,Bの間に
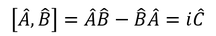
という関係があるとしよう。ここで、
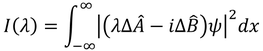
この積分を計算していく。
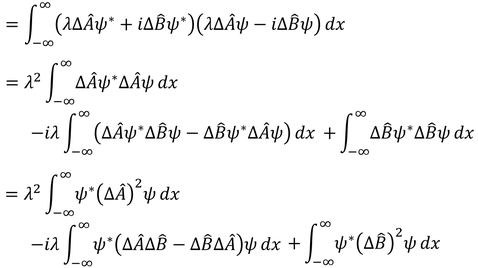
1つ目の積分はAの分散の期待値、3つ目の積分はBの分散の期待値を表している。2つ目の積分を考えるために( )の中身を考えると、
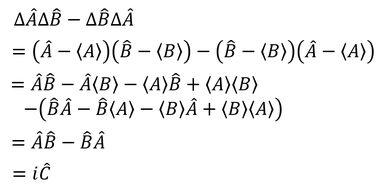
となるので、

となる。この結果が0以上になるためには、判別式が0以下でなければならないので、
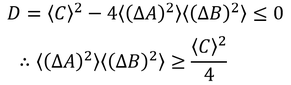
が成立する。このことから、ハイゼンベルクの不確定性原理の導出ができる。
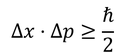
ここで、エネルギーEと時間tの間にも

このように、位置、運動量と同様の関係があることから、不確定性関係
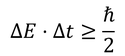
があることが分かる。
