解析力学

一般化座標　←→　変分原理

　ラグランジアンが直接時間ｔを含まないとき、つまりラグランジアンLが

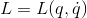
であるとき、全微分は

だから、Lをｔで微分すると、

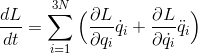
である。ここで、右辺第1項にラグランジュ方程式を使って、

と変形できるので、

になる。この式は、(　)の中の物理量が保存されていることを示している。

であるとき、運動エネルギーTが

と表されるから、

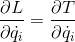
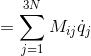
であり、

であるから、

である。これは、運動エネルギーTと位置エネルギーUの和であるから、

より、全エネルギーが保存されていることが分かる。

　このように、時間をｔ→ｔ’と変換してもラグランジアンLに変化がないとき、系は「時間対称性がある」という。時間対称性がエネルギーの保存と対応しているわけだ。

　次は、質点の位置をすべて平行移動してもラグランジアンLが変わらない場合を考えて見よう。このとき、系は「並進対称性がある」という。ただし、微小な変化δqを考えよう。

このとき、ラグランジアンが変化しないということだから、

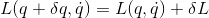
という関係について、

が0であるということである。ラグランジュ方程式を使えば、

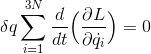
となり、

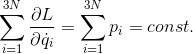
運動量の総和が保存されていることが分かる。

　このように、ある微小変化についてラグランジアンが変化しないとき、それに対応した保存量が存在するというきまりを、ネーターの定理という。

　それでは、質点すべてをｚ軸を中心に回転させたとしてもラグランジアンが変化しない場合を考えよう。

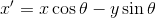
このとき、角度が微小であれば、θ→δθとして、

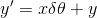
という変換になる。だから、

について、

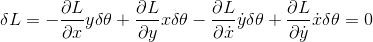
であるということで、

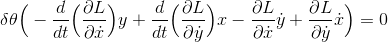
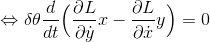
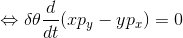
になる。（　）の中身は、角運動量のｚ成分である。

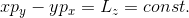
同様にして、ｘ軸、y軸の周りに質点を回転移動させて計算すれば、x成分、y成分についても同じことが言えるので、

よって、系が回転対称であるとき、角運動量が保存されることが分かった。