統計力学

→ ボルツマンエントロピー

　統計力学というのは、熱現象を、ミクロな粒子の集まりから考察しようとする分野だ。まずは熱力学の復習と、統計力学の導入として面白い話を紹介しよう。

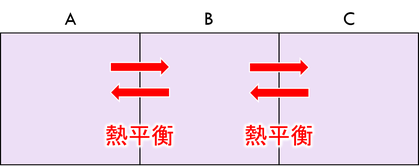
　温度の異なる物体を接触させてしばらく置くと、やがて同じ温度になる。この状態を「熱平衡」と呼ぶ。物体AとB，BとCが熱平衡状態であるとき、物体AとCも熱平衡状態であるといえる。このきまりを、「熱力学第0法則」と呼ぶ。

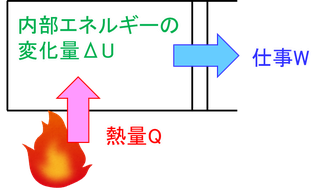
　熱を吸収した物体は、その熱量Qを仕事Wに変え、残りのエネルギーを内部エネルギーとして蓄える。内部エネルギーの変化をΔUと表すと、この間には、

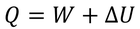
という関係が成り立つ。熱や仕事をエネルギーの形態の一つだと考えると、この式は、広い意味でエネルギー保存則を表していることが分かる。このきまりを「熱力学第1法則」と呼ぶ。

　仕事を取り出すためには内部エネルギーを消費したり、熱量を加える必要があるため、無から仕事を取り出すことはできない。この実現不可能な熱機関を、（第1種）永久機関という。

　熱量や仕事、内部エネルギー変化の微小量をそれぞれd'Q, d'W, dUとすると、熱力学第1法則は

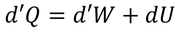
となる。d'Qとd'Wのdに「’」がついているのは、熱量や仕事はもともと物体の状態が変化するときにしか表せない量で、ある1つの状態だけで定まる内部エネルギーとは異なるものなので、内部エネルギーの微小変化量dUとは区別して表している。d'Qやd'Wは単なる微小量だと考えておいて欲しい。

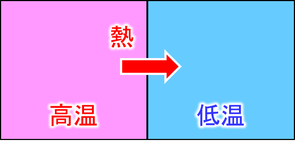
　熱は高温物体から低温物体へ移動する。このきまりを「熱力学第2法則」という。次の内容と区別して、クラウジウスの原理と呼ぶこともある。

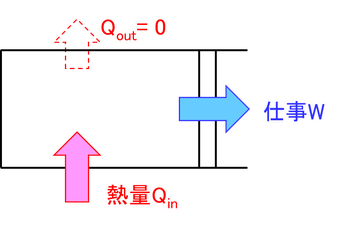
　一般的に、熱機関は吸収した熱の一部を仕事に変え、残りの熱を捨てている。吸収した熱量Q_inに対する仕事Wの比W/Q_inを熱効率と呼び、もし捨てる熱量が0であれば、熱効率は100%ということになる。熱効率が100%であれば、仕事として取り出したエネルギーをすべて回収することで、再び全く同じサイクルを回すことができる。このような機関を、第2種永久機関という。しかし、このような熱機関は不可能であることが知られており、このきまりも「熱力学第2法則」という。上記の内容と区別して、トムソンの原理と呼ぶこともある。

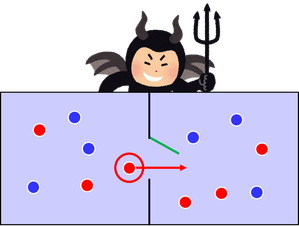
　容器の中にある温度の気体を入れ、中央を仕切る。温度が一定であっても気体の分子は分子ごとに速さが違っている。ここで、もしもそんな気体の様子を「見る」ことができる存在がいたらどうだろうか。この悪魔は左側から速い分子がやってきたら仕切りの窓を開けて右側へ通し、右側から遅い分子がやってきたら今度は左側へ通す。そんなことが可能ではないだろうか。この存在は、考案者の名前から「マクスウェルの悪魔」と呼ばれている。

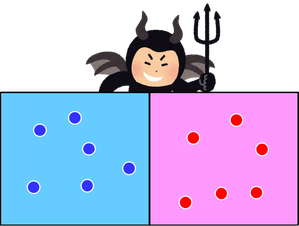
　悪魔がこの操作を繰り返すことで何が起こるかというと、容器の右側が速い分子ばかりに、左側が遅い分子ばかりになるということだから、つまり元の同じ温度の気体を、高温と低温に分けることができるのだ。悪魔は気体を見て窓を開け閉めするだけで、気体対して全く仕事をしていない。だから、悪魔の存在を許すことで熱力学第2法則、クラウジウスの原理を破ることができるというわけだ。

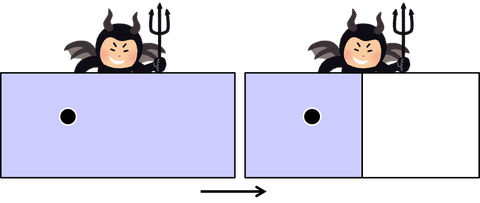
　もう1つ熱力学第2法則が破れる例を紹介しよう。分子が1つだけ入った容器を考える。悪魔はこの分子の位置が右か左かを「見る」ことができる。分子を観測した悪魔は、中央に仕切りを下ろす。

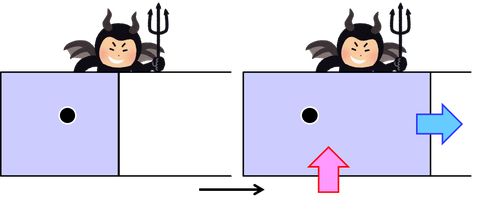
　その後、分子が左側にいる場合は中央の仕切りを右側へ、分子が右側にいる場合は仕切りを左側へ動かす。気体の温度が変わらないように仕切りを動かせば、この気体は、外部から熱を吸収し、そのまま仕事に変える熱機関と見なすことができる。仕事を取り出した後の気体は元と同じ状態になっている。このサイクルでは気体が熱を放出していないため、熱効率は100%になっているのだ。こうして、熱力学第2法則、トムソンの原理を破ることができるのだ。この熱機関を、考案者の名前からシラードのエンジンと呼ぶ。

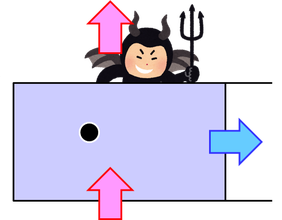
　悪魔の存在と熱力学第2法則は明らかに矛盾する。ではどこがおかしいのか。マクスウェルが悪魔の存在を思いついたのが1871年、シラードがエンジンを考えたのが1923年のことである。その後、1956年にブリルアンらは悪魔が分子を「見る」ときに熱を外部へ放出しているのではないかと考えた。悪魔を機関の一部と見なすと、これによって熱力学第2法則は保たれる。

　ところが1973年、矛盾は解消されていないことが分かった。熱を放出せずに「見る」方法が見つかったのだ。これにより、解消されたと思われていた矛盾が復活することとなった。

　これが解消されたのは1982年のことだった。ベネットは悪魔が分子を「見る」ときに熱を放出するのではなく、見て記憶した情報を「忘れる」ときに熱を放出しなければならないことに気付いたのだ。熱機関がサイクルを行うためには、元の状態に戻る必要があるのだった。だから、見て記憶した情報を忘れなければならなかったというわけだ。