ボルツマン分布
前回は、気体分子の速度成分が独立で対称性があるという仮定に基づき速度分布を導いた。今回は、確率・統計的な考え方を利用して速度分布を導いてみよう。
速度空間と微視的状態数
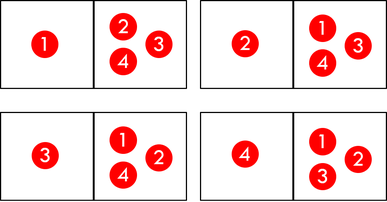
4個の分子を1個と3個に分類する方法の数は、4通りである。
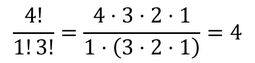
4個の分子を2個と2個に分類する方法の数は、6通りである。
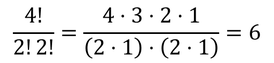
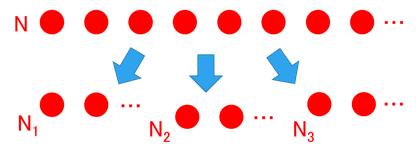
一般に、N個の分子をN1,N2,N3,…に分類する方法の数は、
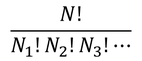
となる。

速度空間内で、分子が取り得る微視的状態数Wを求めたい。無限にありそうな気がするが、速度空間を体積V1,V2,V3,…に分割すると、その内部で分子が取り得る状態の数は、その体積に比例していると考えることができる。そこで、それぞれの領域内で分子が取り得る状態の数を、V1,V2,V3,…と表すことにすしよう。
N個の分子を2か所に分類する方法の数は、2^N通りであり、Ni個の分子をVi個の取り得る状態に分類する方法の数は、Vi^Ni通りである。そして、N1,N2,N3…個の分子をそれぞれV1,V2,V3,…個の状態に分類する方法は、合わせて
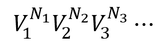
通りとなる。
ここで、N個の分子をN1,N2,N3,…個に分ける方法の数が
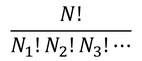
だったから、N個の分子の微視的状態数Wが、

と表せることがわかる。
マクスウェル・ボルツマン分布
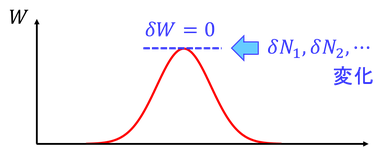
目的は、存在確率が最大になるときのN1,N2,N3,…を求めることである。これは、Wを最大にするようなN1,N2,N3,…を求めることに等しい。N1,N2,N3,…をわずかに変化させたときのWの変化量δWを考え、δW=0になるようなN1,N2,N3,…を探せばいい。δWを「変分」と呼ぶ。
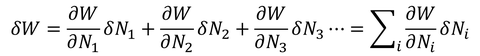
ただ、Wのままでは計算がしにくいので、logWを考えよう。
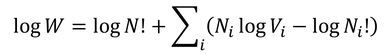
ここで、logN!にスターリングの公式

を使うと、
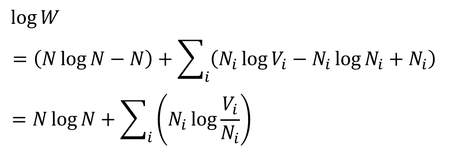
となる。ただし、
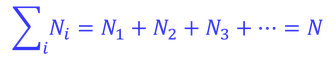
である。
では、logWの変分δlogWを考えよう。
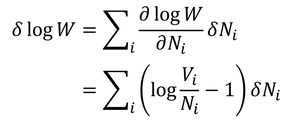
これが0になるときのNiを求めればいい。ただし、N1,N2,N3,…は独立ではなく、N1を変化させるとN2,N3,…も変化してしまう。つまり、

という条件を考慮する必要がある。さらに、孤立した容器内の内部エネルギーは気体の状態によって変化してはいけないから、各微小領域のエネルギーの和が一定であるという条件も必要になる。

各領域における分子のエネルギーをεとしている。この2つの条件を考えつつ、logWが最大になるようなN1,N2,N3,‥を求めなければならない。
「ラグランジュの未定乗数法」を利用しよう。NもEも変化しないのだから、2つの追加条件の変分は0にならなければならない。
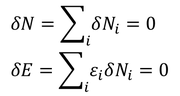
あとは連立方程式を解く要領で、この2つの式に適当な定数α',βを掛け、δlogWから引く。
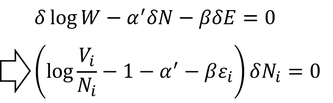
これが解くべき式だ。よって、
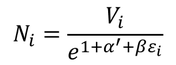
を得る。ここで、微小領域Viに含まれる粒子の割合を
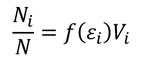
と表すことにしよう。すると、いま求めたNiの式から、
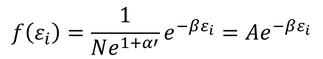
こうしてf(ε)の形が分かる。
いま、各領域に含まれる分子の持つエネルギーεを
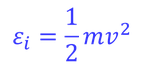
とすることで、
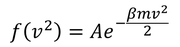
となる。これは、前回導いたマクスウェルの速度分布
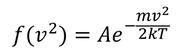
である。このことから
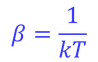
を求めることもできる。この値を用いることで、

を得る。この式は、分子がエネルギーEを持つ確率がe^(-E/kT)に比例することを示している。今回はマクスウェルの速度分布を導きたかったのでエネルギーとして運動エネルギーのみを用いたが、位置エネルギーUがあっても構わない。マクスウェルは前回の方法で導き、ボルツマンは今回のように確率的な考え方から導いた。この分布を「ボルツマン分布」や「マクスウェル・ボルツマン分布」という。
調和振動子の平均エネルギー

ボルツマン分布を利用して、単振動をする粒子の平均エネルギーを求めてみよう。復元力をKxとすると、力学的エネルギーEが
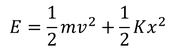
と表せる。ボルツマン分布によると、エネルギーEを持つ粒子の存在確率がe^(-E/kT)に比例するから、確率を
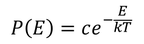
と表すことにする。定数cは、すべてのx,vについて足し合わせた結果が1になるということから、求められる。

ゆえに、確率P(E)は
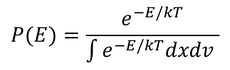
となる。
これを使って、平均エネルギーを求めよう。
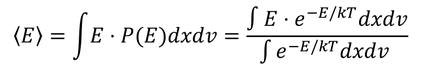
分母は、

分子は、

より、
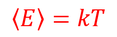
平均エネルギーが求められた。計算の途中で、公式
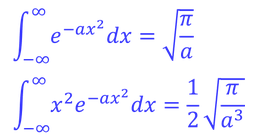
を利用した。
