ボルツマンエントロピー
熱現象をミクロな視点から詳しく見ていく分野が統計力学である。今回は、熱力学第2法則について深く掘り下げてみよう。
エントロピー
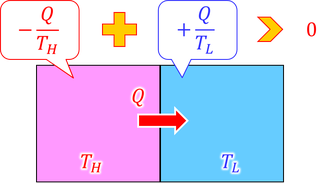
熱は高温物体から低温物体へ移動する。このときの熱量をQとすると、高温物体は熱量Qを失い、低温物体は熱量Qを受け取るが、これらを合わせると熱量は変化しない。これを、「熱量の保存」という。
では
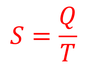
はどうだろう。高温物体の温度をTH,低温物体の温度をTLとしてその変化を足すと、
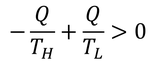
正の値となる。Sを「エントロピー」と呼び、熱的に遮断された領域において、自然はエントロピーが増える方向に変化する。このことを「エントロピー増大の法則」と呼ぶ。
また、熱量の微小変化をd'Qとすると、エントロピーの微小変化量dSは
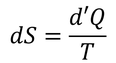
となる。この式および、微小仕事d'W
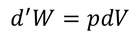
を用いると、熱力学第1法則の式を
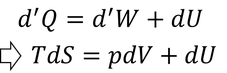
と、状態量のみで書き変えることができる。
微視的状態数
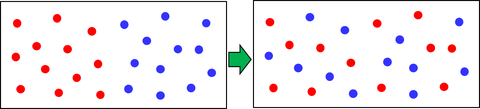
熱が移動することで高温物体のエネルギーが減少し、低温物体のエネルギーが増加する。十分な時間が経過すると内部エネルギーが等しくなり、温度が一定となる。極端ではあるが、この様子を速い分子と遅い分子に分けて表したのが上の図だ。2種類の分子が左右に偏っていた状態から、バラバラに分布した状態への変化が見て取れるだろう。バラバラになるとエントロピーが増加することから、エントロピーを「乱雑さ」と表現することもある。
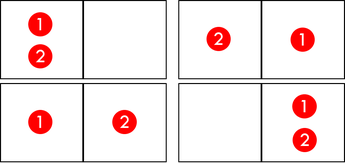
分子の配置パターンを考えてみよう。例えば、1個の分子を左右に分配する方法は、右か左の2通りがある。分子が2個なら、その2倍で4通りがある(上図)。分子が3個なら8通り、4個なら16通りの配置パターンがある。つまり、分子がN個なら、
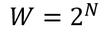
通りの分子の分け方があるわけだ。このの分け方をそれぞれ分子の「微視的状態」、その数Wを「微視的状態数」という。
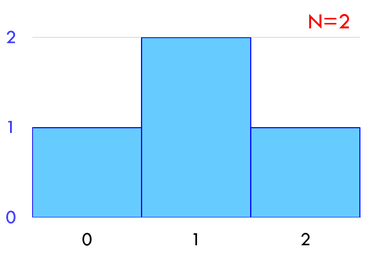
分子が2個のとき微視的状態数は4通りだが、2個の分子が左側へ集まるのは1通り、1個ずつに分かれるのが2通り、右側へ集まるのが1通りである。分子の配置をこのように見たとき、これを「巨視的状態」と呼ぶことにしよう。巨視的状態として左側の容器内の分子の数を横軸に、そのときの微視的状態数を縦軸に取ったグラフが上の通りである。
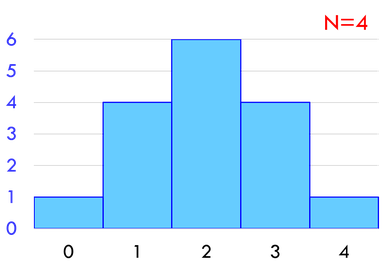
分子の数を4個のとき、左右2個ずつに分かれる微視的状態数は6通りである。つまり、左右に分かれるときの6倍起こりやすいということになる。
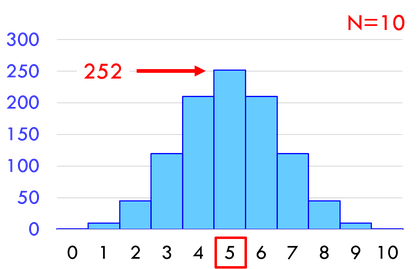
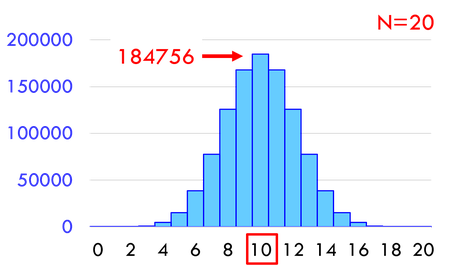

10個の分子が5個ずつに分かれる微視的状態数は252通り、20個の分子が10個ずつに分かれる微視的状態数は18万4756通り、100個の分子が50個ずつに分かれる微視的状態数は約10^29通りも存在する。右や左にすべての分子が収まる確率と比較すると、とてつもなく起こりやすいことが分かるだろう。だから、偏った状態からバラバラになることはあっても、その逆はほぼあり得ないのだ。
ボルツマンの関係式
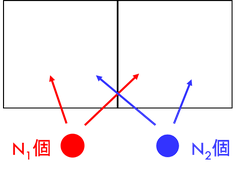
続いて、N1個、N2個の2種類の分子をそれぞれ左右に分配するときの微視的状態数Wを考えよう。それぞれの微視的状態数は

であり、合わせてN1+N2個の分子があるから、
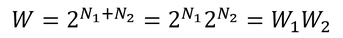
のように、全体の微視的状態数Wは、それぞれの分子の微視的状態数の積W1W2になっていることが分かる。
ところで、熱平衡状態(同じ温度)になるまでのエントロピー変化Sは、それぞれの容器内のエントロピー変化S1,S2を足し合わせることで求めた。
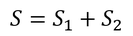
このことから、微視的状態数の積W1W2の増加が、エントロピーの和S1+S2の増加に対応していることが予想できる。そこで、エントロピーSと微視的状態数Wをつなぐ式として、

が生まれた。これを「ボルツマンの関係式」という。エントロピーの和S1+S2を計算してみると、
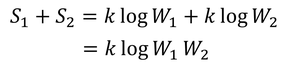
となり、エントロピーの和S1+S2と微視的状態数の積W1W2の大きさが対応していることが分かる。
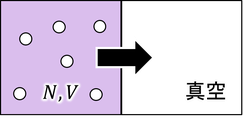
ボルツマンの関係式を別の方法で導いてみよう。N個の分子を体積Vの容器に入れ、自由断熱膨張させて体積を2倍にする。その間のエントロピー変化を求めるのだ。エントロピーの計算は、可逆過程で行わなければならないから、等温過程に沿って計算すると、
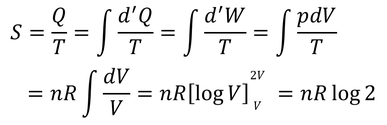
となる。ここで、アボガドロ定数NAと分子数Nを用いて
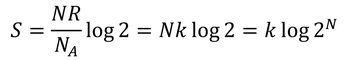
と書き変える。途中で置いた

を「ボルツマン定数」という。ところで、2^NはN個の分子を左右に分配するときの微視的状態数Wのことだったから、

これで、ボルツマンの関係式が導けた。
熱力学第3法則
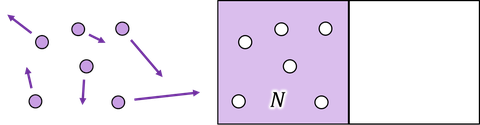
ところで、初めの状態はN固の分子すべてが左側にいたわけだから、状態数はW=1である。よって、ボルツマンの関係式からエントロピーはS=0となる。このようにエントロピーは、ある状態を基準(S=0)として、そこからの変化に沿って計算される量なので、基準を定める必要があるのだ。
しかし、体積Vの中にいる分子は、細かく見ればすべてが異なる位置にいて、様々な速度で運動をしている。このようなところまで見ると、状態数は1とは言えない。

そこで、絶対的な基準を考えることにする。位置関係を固定するためには、結晶を、特に欠損などのない理想的な「完全結晶」を考えればいい。熱運動を停止させるためには、「絶対零度」を考えてやればいい。つまり、
- 完全結晶のエントロピーは、絶対零度で0である。
このエントロピーの基準を、「熱力学第3法則」という。
