相対性理論

相対性原理 ←→ 時間と空間

　波動方程式

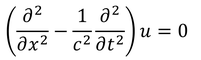
に現れる波の速さｃは、波を伝える物質である媒質に対する速さである。そう考えると波動方程式が前回紹介したような形になる。ところが光には媒質が必要ない。では、光の速さは何に対する速さなのだろうか。

 発想を変えよう。光に媒質が必要ないのではなく、宇宙は未知の媒質で満たされていて、光はその媒質によって伝えられていると考えるのだ。この未知の媒質を「エーテル」という。

　このエーテルの存在を測定する試みとして、マイケルソンとモーリーの実験があるので紹介する。地球は太陽の周りを公転しているから、その際にエーテルの”風”を受けているはずだ。これを図のような装置で測定することを考えるのだ。

　まず光の経路をハーフミラーで直交する2方向に分ける。一方はエーテルの風に対して平行、他方は垂直な方向にしておく。この光は鏡で反射して戻ってくるので、干渉して明るくなったり暗くなったりする。この性質を利用すると、風による影響を考えることができる。

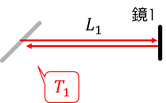
　鏡1で反射して戻ってくるまでの時間をT1とすると、鏡まではエーテルの風に逆らって光は進み、鏡で反射した後はエーテルの風に乗って進むから、

である。ここで

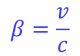
とすると、β^2は非常に小さいはずだから近似が使える。

と直せる。

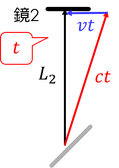
　鏡2で反射して戻ってくるまでの時間をT2とする。片道の時間tは上右図より

である。T2はその2倍だから、

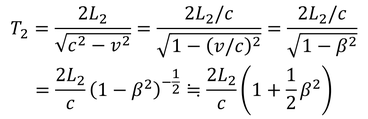
であることが分かる。

　T1とT2の差は、

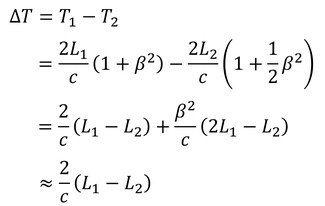
となる。β^2は非常に小さいので、光の時間差はL1とL2の差でほとんど決まってしまうということが分かる。このままではエーテルの風の影響が分からない。

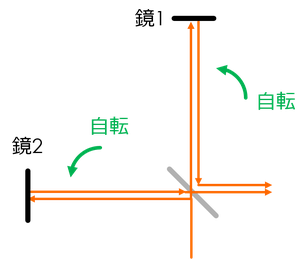
　ここで、自転によって装置全体が90°回転したあとの光の時間差の計算もしてみよう。鏡1,2で光が反射して戻ってくるまでの時間はそれぞれ

だから、その差は

となる。

　ΔTとΔT'の差を計算してみると、

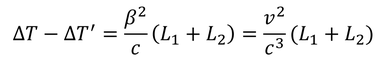
のように、L1-L2の項が消去できる。もしもこの値が測定できれば、そこからエーテルの風の速さｖが得られるはずだ。

　マイケルソンとモーリーがこの実験を行った結果、誤差以上のエーテルの風の影響は得られなかった。この結果を受けてフィッツジェラルドとローレンツは、エーテルに沿って運動する場合、距離が縮むと考えた。これを「ローレンツ収縮」と呼ぶ。

　T1とT2をもう一度書くと

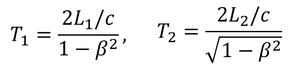
だから、L1を

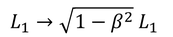
とすればT1とT2は一致する。距離が縮んでしまうため、エーテルが観測できないと考えたのだ。

　ここで登場するのがアインシュタインだ。アインシュタインは16歳のとき、光の速さで鏡を追いかけたら顔が映らなくなるのだろうかと考えた。鏡に光が映るのは顔から出た光が鏡に到達し、反射した光を見ているからだ。だから顔から出た光を同じ速さで追いかけたら映らなくなるのではないかということだ。しかし、アインシュタインにはそうは思えなかった。そこから、

• 光にとって特別な慣性系は存在しない。
• どの慣性系で観測しても（真空中の）光の速さは同じ。

という考えに達した。これを「光速度不変の原理」と呼ぶ。地上で静止していても、電車に乗っていても、飛行機に乗っていても宇宙船に乗っていても、光は同じ速さなのだ。だから、光の波動方程式に現れる速さｃは、誰から見てもｃということ。エーテルはなくても問題がなかったのだ。

　光速度不変の原理により、光の波動方程式が慣性系に寄らないから、光や電磁気に関する法則は慣性系によらず同じ形で表されることになる。また、運動の法則も慣性系によらず同じ形で表されることは前回確認した（ガリレオの相対性原理）。アインシュタインはこれらの内容を発展させ、

• ”すべての物理法則”は慣性系によらず同じ形である。

と考えた。これを「特殊相対性原理」と呼ぶ。光速度不変の原理と特殊相対性原理という2つの原理からスタートし、アインシュタインは「相対性理論」を作り上げたのだ。