事象の地平面
アインシュタイン方程式を解いてみよう。いくつか代表的な解があるが、今回は中心に重たい天体があり、その周囲に時間的に変化しない静的で球対称な時空が広がっていると仮定する。このようにして得られる解をシュバルツシルト解と呼ぶ。
球対称時空
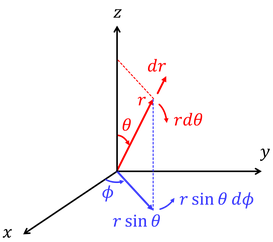
球対称な時空を考えたいから、今回は極座標を用いるのが便利だ。

すると、ミンコフスキー時空での世界間隔ds^2は次のようになるので、

ミンコフスキー計量は
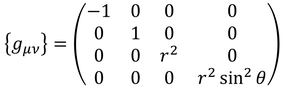
となる。このことを踏まえて、曲がった時空を表すために、世界間隔を

と書き変えよう。今回は球対称な時空を仮定しているから、θ成分とφ成分に変更はないはずだ。すると、計量は

になる。この逆行列

もあとで利用するので紹介しておこう。
シュバルツシルト解
いよいよアインシュタイン方程式を解くことを考える。宇宙全体の運動を考えているわけではないから宇宙項を無視し、アインシュタインテンソルとエネルギー運動量テンソルの添え字は下に付けておく。

アインシュタイン方程式を解くとは、この方程式を利用して上述の関数A,Bを求め、時空の曲がり具合を知ることである。
まずは、時空が静的で時間変化しないと仮定しているから、計量の時間微分が0

であることに注意して、クリストッフェル記号

の各成分を計算する。μ=0のときは
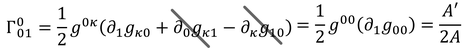
μ=1のとき

μ=2のとき
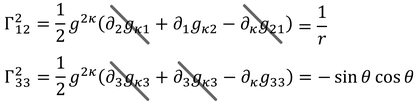
μ=3のとき
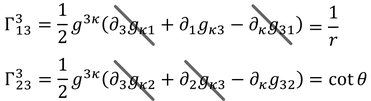
ただし、

である。
次はリッチテンソル

を計算する。0でないのは、00成分
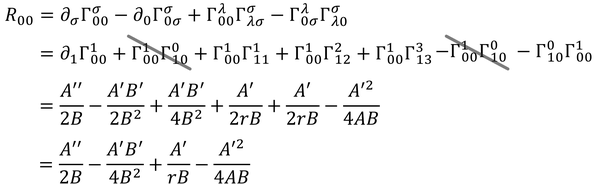
11成分

22成分

33成分

のみである。
これでスカラー曲率
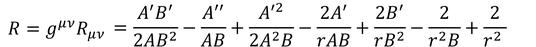
が得られるので、続いてアインシュタインテンソル

を求める。00成分

11成分

22成分
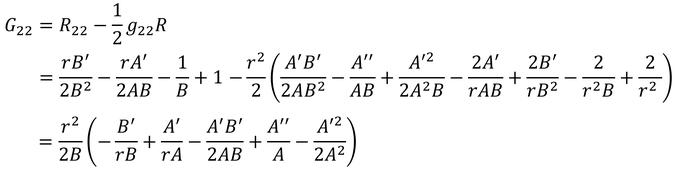
33成分
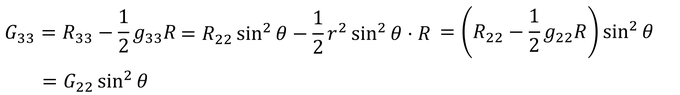
ここで、重たい天体の周囲には真空が広がっているとすると、エネルギー運動量テンソルの各成分は0になるから、アインシュタイン方程式より、アインシュタインテンソルの各成分も0になる。

そこで、

という式を考え、計算すると、
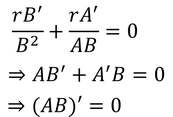
となることから、AとBの積が一定であることが分かる。これを定数Cとおこう。

ここで、関数A,Bは無限遠方(r=∞)でミンコフスキー時空と等しくなるため、A(∞)=1,B(∞)=1でなければならない。このことから、C=1だと分かる。よって、B=1/Aである。
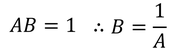
すると、
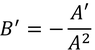
だから、これを用いてアインシュタインテンソルの22成分を書き変えることで、


という関係が得られる。積分すると

となる。ここで、定数部分を
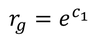
とおいてさらに積分すると

となるが、無限遠方(r=∞)でA(∞)=1であることから、定数がC2=1と決まる。

こうして、アインシュタイン方程式の解の一つでとして、次のような世界間隔が得られる。

これを、シュバルツシルト解と呼ぶ。
事象の地平面とブラックホール
シュバルツシルト解には2つの特異点がある。1つめはr=0で、これは中心の重い天体の位置である。2つめはr=r_gで、この距離をシュバルツシルト半径という。ここで、計量テンソルgの00成分は
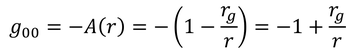
であるが、これをミンコフスキー計量ηの00成分からのわずかなずれh_00を用いて表現すると

だったから、これら2式より

こうしてシュバルツシルト半径が求められる。
シュバルツシルト半径の意味を考えるために、半径方向に運動する光について考えよう。半径方向の運動だからθ成分とφ成分が無視でき、光の場合、世界間隔は0になる。

この式より、
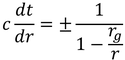
を得る。この関係から、光の運動を時空図に表したときの傾きが得られる。

青色のグラフは光が中心に向かうときの運動を表している。このグラフから、シュバルツシルト半径に近づくにつれて徐々に遅くなり、どれだけ時間がかかってもシュバルツシルト半径よりも内側には入れないことが分かる。赤色のグラフは光がシュバルツシルト半径から外に向かうときの運動を表していて、徐々に速くなっていく様子が分かる。

シュバルツシルト半径よりも内側についても同様にグラフを描くと上図のようになる。ここで、世界間隔が負になるような2点を考えよう。この関係を時間的と呼び、過去と未来を表している。シュバルツシルト半径よりも外側(r>rg)では
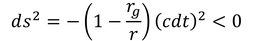
となる2点が時間的、シュバルツシルト半径よりも内側(r<rg)では

となる2点が時間的である。この結果から分かるのは、シュバルツシルト半径よりも内側では、物体は決してその場にとどまることが許されず、必ず中心へ向かうことだ。もちろん、光も例外ではない。
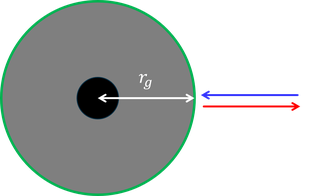
世の中で最も速い光であってもシュバルツシルト半径の内側に入ることはできないし、内側から外に出てくることが許されない。つまり、内側の情報を見ることができない。この意味で、中心からシュバルツシルト半径の距離にある点の集まりを事象の地平面と呼ぶ。太陽だと約3km,地球だと約9mmになるが、世の中には事象の地平面よりも内側に収まっている天体もあり、この天体こそがブラックホールである。
