気体の状態方程式

前回はどちらかといえば液体や固体をイメージして話をしたけれど、ここから先はずーっと気体について考える。気体が液体や固体と大きく異なるのは、体積変化が大きいということと、目に見えないということ。ときどき小さな粒子が動き回っている様子を想像してみよう。きっと理解の助けになるはずだ。
気体の圧力

断面積Sの円筒形の容器に気体を入れて、滑らかに動くピストンでふたをする。このとき、ピストンには容器内の気体と容器外の気体が押す力がはたらき、静止しているとすればこれらの力はつり合っている。
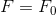
ここで圧力pの話を思い出そう。圧力とは、断面積Sの面にはたらく単位面積当たりの力のことだった。
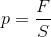
この関係を使って力FとF0の関係式を書き変えると、
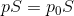
になるから、
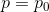
容器内外の気体の圧力の関係を導くことができる。

また、ピストンの質量がmのとき、この容器を縦に置いたとすると、容器内の気体の圧力pは力のつり合いの関係を使って、
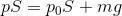
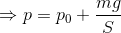
のようにして求めることができる。
ボイル・シャルルの法則

温度一定のもとで容器内の気体の体積を小さくしていくと、容器内の圧力は大きくなっていく。このときの体積Vと圧力pは反比例の関係になっていて、


この関係が成り立つことをボイルの法則という。

圧力一定のもとで容器内の温度を上げていくと、気体の体積は大きくなっていく。このときの絶対温度Tと体積Vは比例の関係になっていて、


この関係が成り立つことをシャルルの法則という。ただし、温度は絶対温度でなければ成り立たないので気を付けよう。
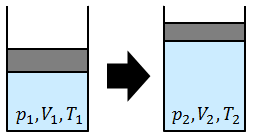
ボイルの法則とシャルルの法則の式は次のように1つにまとめることができて、
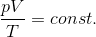
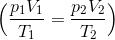
この関係が成り立つことをボイル・シャルルの法則という。ただし、温度は絶対温度でなければ成り立たないので注意。
気体の状態方程式
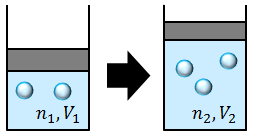
ボイル・シャルルの法則を少し発展させよう。実はボイル・シャルルの法則は、気体の粒子数が一定のもとで、温度・圧力・体積を変化させた場合にしか成り立たない。例えば、温度や圧力一定のもとで粒子数を変化させると、体積は増加する。このとき、粒子数Nと体積Vの間には比例関係があるので、
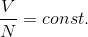
この関係もボイル・シャルルの法則に組み込んでしまえば、
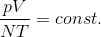
という式になる。
ただし、気体の粒子数Nはとんでもなく多いので、6×1023個の粒子をひとまとめにして、このまとまりがいくつあるかで考えるのが一般的だ。このまとまりを物質量といって、n〔mol〕と表す。
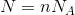
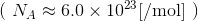
すると、今の式は
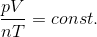
になる。
ここで、p〔Pa〕, V〔m3〕,n〔mol〕, T〔K〕という単位を使うことにすると、定数部分が

と決定され、

という式を導くことができる。この式を気体の状態方程式といい、定数Rを気体定数という。
