偏微分
熱力学の分野では非常にたくさんの変数が出てくるので、そろそろ混乱してきたころではないだろうか。例えば、気体の状態方程式
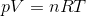
を考えただけでも、4つの変数が登場する(p,V,n,T)。このうち、物質量nが変化する場合はあまり扱わないので考えないことにするが、まだ3つの変数が残る。

3変数関数は非常に分かりにくい。そこで、このうち1つを一定として、残り2つの変化を考えることにしよう。例えば、定圧変化では圧力pが一定で、体積Vと温度Tが変化する。このときの体積変化をΔV,
温度変化をΔTと表すと、状態方程式より


という関係が成り立っていることが分かる。
さて、ここからはT,Vの微小変化量を考えよう。といっても難しい話ではなくて、単にΔTを微小量dT, ΔVを微小量dVと書き変えるだけだ。

これを微分といった。ただし、普通の微分とは違う。なぜなら、今は本当は変数であるはずの圧力pを「定数とみなして」考えてきたからだ。このような微分を偏微分と呼び、普通の微分とは区別して次のように表す。
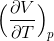
添え字は省く場合もあるが、熱力学の分野では定数とみなした変数をこのようにはっきりと記述する場合が多い。
偏微分

ここで偏微分の定義を示しておこう。関数z(x,y)をxで偏微分するとは、yを固定したときのz-xグラフの傾き
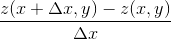
を考えて、Δxを限りなく0に近づける(Δx→0)ということなので、
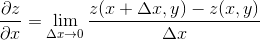
ということになる。普通の微分の定義と見比べてみよう。
問題
(1) z(x,y) = 3xy + y2 をxで偏微分せよ。
定義式に代入して解いてもいいけれど、普通の微分が身についていれば、yを定数とみなして計算してしまえばいい。

(2) z(x,y) = 3xy + y2 をyで偏微分せよ。
今度はxを定数とみなして計算すれば、

全微分

yを固定して描いたz-xグラフについて、xの微小変化量dxに対応したzの微小変化量は、(グラフの傾き)×(dx)となるから、
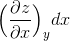
と表現できる。
ところで、このzの微小変化量はdzと表してもよいのだろうか。答えは、よくない。なぜなら、zは、dxだけでなくdyにも対応して変化するからだ。
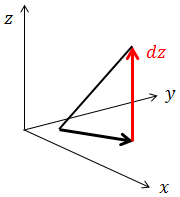

普通は、x,yがそれぞれdx,dyだけ変化したときのzの変化量をdzと表記するので、xの微小変化dxに対応したzの変化量と、yの微小変化dyに対応したzの微小変化量
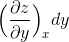
の和を考えなくてはならない。
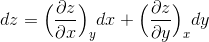
これを、zの全微分という。
問題
気体の圧力pが、体積Vと温度Tを変数に持つ関数p(V,T)だと考えて、その全微分dpを定義に沿って表せ。
解答

状態量

実は、全微分で表すことができる物理量には条件がある。それは、その物理量が経路によって変化しないということだ。例えば、圧力pや体積V、温度Tや内部エネルギーUなどは、いまの状況で決定される量で、以前の経路によって変化したりはしない。このような物理量を状態量と呼び、その微小量は全微分

で表すことができる。
ところが、仕事Wや熱量Qなどはこのように表すことができない。例えば、気体の状態を(p1,V1)から(p2,V2)へ変化させたとき、気体がした仕事Wはp-Vグラフの面積で表されるが、気体の変化のさせ方によって面積Wが異なることが分かるだろう。そこで、WやQの微小量は、そのほかの全微分で書くことのできる物理量と区別して、
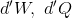
のように「’」を付けて表す。
これらを使うと、熱力学第一法則の式「Q=W+ΔU」を微小量に対する関係式に書き変えることができる。
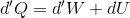
あとで使うので、頭の片隅に置いておいてほしい。
