エントロピー
熱力学第二法則は、熱現象の方向や性質を表すものだった。今回は、エントロピーという物理量を使って、熱現象の方向を表す方法を考えていく。有名なエントロピー増大則も登場するよ!
カルノーの定理
「2つの熱源の間ではたらく熱機関の効率は、可逆機関Cが最大である。」これをカルノーの定理という。2つの熱源の間ではたらく可逆機関といえばカルノーサイクルしかないので、カルノーの定理は、カルノー機関が熱効率最大であることを述べている。

それでは、カルノー機関の熱効率e'を求めてみよう。まず、熱機関の仕事と熱量の関係
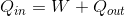
を使って、熱効率eの式を次のように書き変えておく。

ここで、このカルノーサイクルが温度T(H)の高温熱源から熱を受け取り、温度T(L)の低温熱源へ熱を棄てているとすれば、A→Bの等温過程で吸収した熱量Q(in)、およびC→Dの等温過程で放出した熱量Q(out)は、熱力学第一法則と以前解いた問題の解答より、
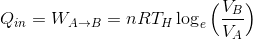

と計算できる。また、これらの式より、
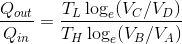
という関係が分かる。続いて、B→CおよびD→Aは断熱過程だから、ポアッソンの式が使えて、
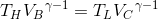

また、これらの式より、
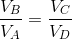
と言う関係が分かるから、これを前の式へ代入すれば、
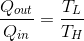
となる。以上より、カルノー機関の熱効率e'が、
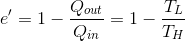
のように、2種類の熱源の温度だけで表されることが分かった。
ここでカルノーの定理より、カルノー機関の熱効率e'が他の熱機関の効率eよりもいい(e'>e)のだから、

という関係が成り立つ。さらに、一般の熱機関の中にカルノー機関自身も含めると、この関係式は

となる。等号成立は可逆機関(カルノー機関)の場合。
クラウジウスの不等式
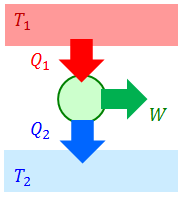
温度T1の高温熱源と温度T2の低温熱源を考える。いま、一般の熱機関が高温熱源から熱量Q1を受け取り、低温熱源へ熱量Q2を棄てているとすれば、カルノーの定理(e'≧e)より
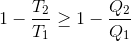
という式が成り立つ。等号成立は可逆機関の場合。
さて、この式を書き変えると、

となるが、熱機関が熱を吸収した場合をQ>0とし、熱を放出した場合をQ<0として表すことにすれば、今の式は
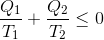
と書き変えられる。こうすると、熱機関が3種類以上の熱源から熱のやり取りをする場合に、

という関係式が現れることが分かりやすい。
さらに、熱源の温度差が微小で連続的な場合には、これを積分の形で表すことができて、次のようになる。

積分記号の〇は積分経路が閉じていることを示しており、この式をクラウジウスの不等式という。ただし、等号成立は可逆機関の場合。
エントロピー
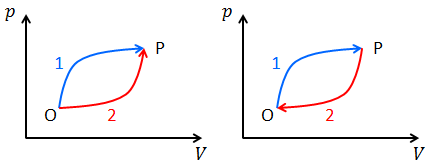
状態Oから状態Pへの可逆変化を2種類考え、それぞれ「過程1」「過程2」とする。いま、状態Oから状態Pへ過程1で変化させ、その後、過程2の逆変化で状態Oに戻すというサイクルをたどれば、クラウジウスの不等式の等式が成り立つから、
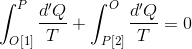
という式が作られる。ここで、積分範囲を逆転させると符号が逆転することに気を付けて式変形すれば、

になる。両辺を比較すると、違いは積分経路だけである。これはつまり、
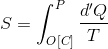
という値が変化の経路によらないことを意味している。物理量Sが経路によらずに決まるということは、このSは状態量である。これ
を、状態Pのエントロピーという。ただし、この積分計算は可逆過程[C]で行われなければならない。
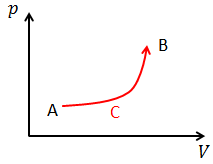
また、エントロピーは状態量なので、A点やB点における値は経路によらない。よって、A点,B点におけるエントロピーが
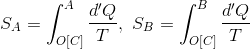
と表されるとき、その変化量ΔS(A→B)は、その差
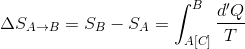
で表すことができる。
エントロピー増大則

次は、状態Aから状態Bへの変化の過程を2種類考え、「過程X」は不可逆変化、「過程C」は可逆変化とする。いま、過程Xで状態Aから状態Bへと変化させ、その後、過程Cの逆変化で状態Aに戻すサイクルをたどれば、クラウジウスの不等式より、

という関係式が成り立つ。ここで、A点,B点のエントロピーをそれぞれSA,SBと書くことにすると、
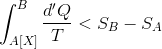
と変形できる。すると、過程Xが断熱変化のときは、d'Q=0より、
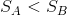
と言う関係を導くことができる。これは、断熱不可逆過程Xにおいてエントロピーが増加することを示していて、このきまりをエントロピー増大則という。
逆に、エントロピーが増大していれば、その過程が断熱不可逆変化であることが分かる。
問題
体積2Vの容器を半分に区切り、片方に気体を入れ、もう片方は真空状態であるとする。この状態から中央の仕切りをはずすと、気体は自由膨張を始めた。エントロピーの変化量ΔSを求めよ。

解答
自由膨張では気体の温度Tは変わらない。また、エントロピーの計算は可逆過程でおこなわなくてはならないから、等温膨張を考えて計算してみる。まず、エントロピーの定義は

であるが、熱力学第一法則より「d'Q=d'W」だから、
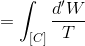
になる。ここで、微小な仕事は「d'W=pdV」と表すことができるから、

である。さらに、気体の状態方程式を用いてpをVで表せば、

となるから、

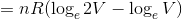

となる。
ΔS>0だからエントロピーが増大している。このことから、この過程が不可逆変化であるということが分かる。
