力と運動

→ 等速直線運動

　物理の世界へようこそ！　物理のことを「カッコいい！」と思ってもらえたら嬉しいな。

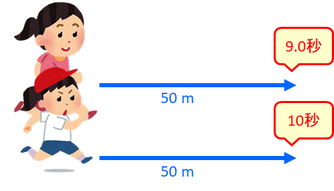
　高校物理は「速さ」から始まる。では速さが何かを離す前に、「速い」「遅い」とはどういうことかについて詳しく見ていこう。例えば、50m走の記録が10秒のAちゃんと10秒のBさんを比べると、「速い」のはBさんだと言える。これは、距離が同じで、かかった時間が短いからだ。

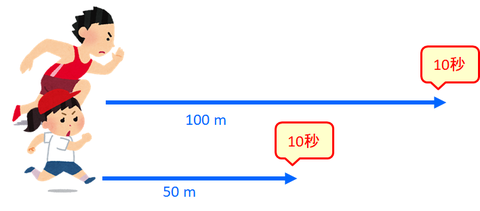
　一方、50mを10秒で走るAちゃんと、100mを10秒で走る陸上選手を比べると、陸上選手の方が「速い」といえる。これは、時間が同じで、走った距離が長いからだ。

　このように、距離と時間のうち、一方が同じ数字なら、もう一方の数字を比較することでどちらが「速い」のかを判断することができる。

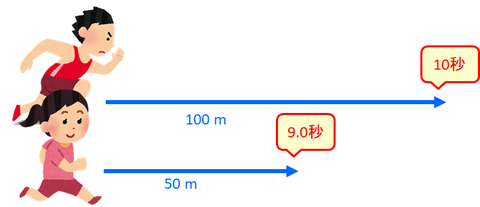
　では距離も時間も違う場合はどうすればよいのだろう。この解決方法は２つあって、1つは「決まった距離を進むのにかかる時間」を比べる方法で、もう1つは「決まった時間に進む距離」を比べる方法だ。1つ目の方法なら時間が短い方が速いといえるし、2つ目の方法なら距離が長い方が速いといえる。このうち、2つめの量のことを「速さ」という。どうして1つ目ではなく2つ目の量を考えるのかというと、「数値が大きい」ほど「速い」といった方が分かりやすいのが理由だと思う。

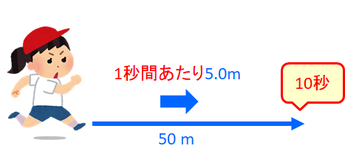
　「決まった時間」のことをこれから物理では「単位時間」と呼ぶことにする。単位時間は1秒でも10分でも1時間でもいいけれど、1秒と1時間をよく使う。

• 「速さ」の定義…単位時間あたりの移動距離

　いま、単位時間を1秒とすると、50mを10秒で走ったBちゃんは「1秒間あたり5.0m」進んでいることになるので、これがBちゃんの「速さ」というわけ。この速さを、単位を付けて5.0m/s（メートル毎秒）と表す。sは秒を表すsecondの頭文字。「/s」は「1秒間あたり」という意味。

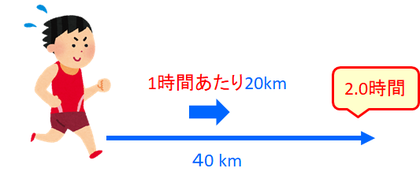
40kmの距離を2.0時間で走ることができるマラソン選手がいるとする。単位時間を1時間とすると、このマラソン選手は、「1時間あたり20km」進んでいることになる。この速さを、20km/h（キロメートル毎時）と表す。hは時間を表すhourの頭文字。「/km」は「1時間あたり」という意味。

　50mの距離を10秒間で走ったAちゃんの速さ5.0m/sは、

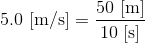
と計算すれば求めることができる。今後、物理では、いろいろな物理量を記号で書いて、それらの関係を表すことになる。試しに速さをv、距離をx、時間をtと表すことにすると、上の関係は、

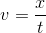
となる。ちょっとカッコよくない？ 

(問) 40kmを2.0時間で走ったマラソン選手の速さは何km/hか。

(答)

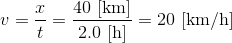
　50mの距離を10秒で走ったAちゃんの速さは「5.0m/s」で、40kmの距離を2.0時間で走ったマラソン選手の速さは「20km/h」となるわけだが、この2種類の速さはどちらの方が「速い」のだろう？　それを知るためには、どちらか一方の単位に合わせてやる必要がある。やってみよう。

① km/h → m/s

　1km=1000m, 1h=3600sだから、

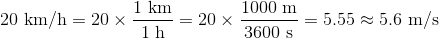
② m/s → km/h

　1m=(1/1000)km, 1s=(1/3600)hだから、

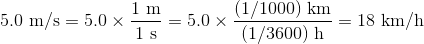
単位をm/sに合わせて比較をすると、Aちゃんは5.0m/sでマラソン選手は5.6m/sだから、マラソン選手の方が速いということが分かる。単位をkm/hに合わせて比較をしても、Aちゃんは18km/hでマラソン選手は20km/hだから、マラソン選手の方が速いということが分かる。

　テレビ中継を見ていて思うけど、マラソン選手ってめちゃくちゃ速いよね。計算してみると、50メートル9.0秒のペースで2時間以上も走り続けてることになるんだよ。

速さに向きを加えた量を「速度」という。例えば、

• 東向きに5.0m/s
• 西向きに3.0m/s

このような量が速度だ。そう考えると速さとは「速度の大きさ」ということになるから、上の例だと5.0m/sや3.0m/sが「速さ」ということになる。

　また、東西や南北、左右といった一直線上の運動の場合、一方を正の向きと定めることで、正と負の符号を使って速度を表すことができるようになる。例えば、東向きを正すると、上の例は

• ＋5.0m/s
• ー3.0m/s

となる。正の符号は省略されることもあるから、東向きを正と決まっていれば5.0m/sだけでもOKだ。

　変位は「位置の変化量」と定義されている。どういうことかというと、x軸上で原点0から50mという位置へ移動したとすれば、その位置の変化量は「+50m」になるということだ。逆向きに、原点0から-30mという位置へ移動したときは、「-30m」となる。