落体の運動
ここからしばらく、重力を受けて落下する物体の運動を見ていくことになる。ただし、初速度の与え方によって、いろいろな運動をするので、順番に見ていきながら、その特徴を覚えてほしい。
自由落下
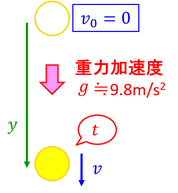
ボールを空中に持ち上げて静かに手を離すと、ボールは初速度0で、鉛直下向きに一定の加速度で加速しながら落下する。この運動を「自由落下」といい、このときの加速度を「重力加速度」という。その大きさは、地球上ではおよそ9.8m/s2である。特有な数値を持つので、これをgと表すこともある。ちなみに自転による遠心力を強く受ける赤道地域は、若干極地域よりも小さな値になっている。また、月面上での重力加速度の大きさは、地球上での約1/6である。
自由落下は等加速度直線運動の特別な運動で、その特徴は
- 初速度v_0が0であること。
- 加速度aが重力加速度g(≒9.8m/s2)であること。
これらに気を付けて、等加速度直線運動の3公式を書き変えると、次のようになる。
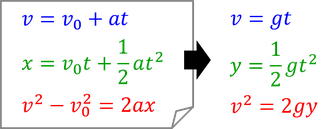
変位xがyになっているのは、縦方向の運動だからそうしているだけだ。
では、自由落下をはじめて1.0秒後の物体の速さvと落下距離yを求めてみよう。1つめの式を使うと
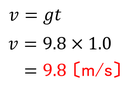
速さvが求められ、2つめの式を使うと

落下距離yが求められる。
鉛直投げ下げ
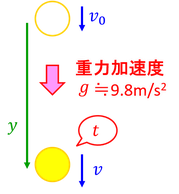
自由落下は初速度が0で落下していく運動であったが、今度は鉛直下向きに初速度を与えたときの運動を見ていこう。これを「鉛直投げ下げ」という。初速度があったとしても、投げ出されたあとの物体の運動は、自由落下と同様に、重力加速度によって等加速度直線運動をする。これをgと書くと、等加速度直線運動の3公式は次のように書き変えられる。
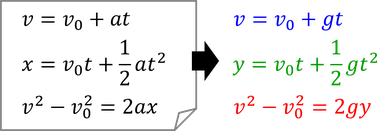
では、計算してみよう。1.0m/sで鉛直下向きに投げ下げられた物体の、1.0秒後の速さvと落下距離yを求めてみる。まず、1つめの式から、
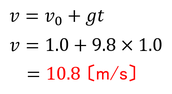
速さvが求められる。次に、2つめの式から、

落下距離yが求められる。
鉛直投げ上げ

ボールを鉛直上向きに投げ上げると、減速しながら上昇し、しばらくすると向きを変えて戻ってくる。このときの加速度は、上昇中も、下降中も鉛直下向きであり、その大きさは9.8m/s2になっている。前回紹介した重力加速度だ。今回も等加速度直線運動の公式を使うことができるが、初速度と加速度の向きが逆向きであることに注意して欲しい。一方を正の向きとすると、もう一方が負の値になる。
鉛直上向きを正とすると加速度が負の値になるので、これを-g表す。すると、等加速度直線運動の3公式は、

となる。

とりあえず計算してみよう。鉛直上向きに初速度9.8m/sを与えたとき、1.0秒後の速度vと変位yを求める。上向きを正とすると、加速度は負の値-9.8m/s2だから、

となる。速度が0であることから、この位置が「最高点」であることがわかる。そして、最高点の高さが4.9mであることも分かる。
続いて2.0秒後の速度vと変位yを求めてみよう。すると、

となる。変位が0であることから、この位置が「元の位置」であることがわかる。そして、元に戻って来たときの速度が、初速度と逆向きで同じ大きさになっていることも分かる。

また、最高点に達する時刻が1.0s,元の位置に戻る時刻が2.0sであることから、上昇時間と下降時間が等しいことも分かる。知っておくと便利だ。
鉛直投げ上げの問題では、いま求めたような「最高点」と「元の位置」について聞かれることが多い。もし、最高点について聞かれたら「v=0」を用い、元の位置について聞かれたら「y=0」を用いて計算すればよい。
例えば、最高点に達する時刻を求めるときは、ひとつめの式を「v=0」として

のように計算する。
元の位置に達する時刻を求めるときは、ふたつめの式を「y=0」として

のように考えればよい。途中でt≠0としたのは、t=0は投げ上げた瞬間のことだからである。この計算からも、元の位置に戻ってくるまでの時間が、最高点に達するまでの時間の2倍になっていることが分かる。
水平投射

ボールや小球に対して、水平方向に初速度を与えると、上図のような運動をする。複雑な運動に感じるが、水平方向の運動だけ、鉛直方向の運動だけに注目すると、
- 水平方向…等速直線運動
- 鉛直方向…自由落下
になっている。このように、放物運動では2種類の運動に分けて考えるようにして欲しい。

では、次のような問題を考えてみよう。ボールに対して、高さ4.9mの位置から水平方向に初速度10m/sを与えた。ボールは前方何mの位置に落下するか。
まず、鉛直方向の運動(自由落下)を考えて、ボールが地面に落下するまでの時間tを求める。

続いて水平方向の運動(等速直線運動)を考えて、1.0秒間に進む距離xを求める。

このように、まず一方の方向の運動に注目して時間tを求め、それをもう一方の方向の運動に用いることで、複雑な問題でも解くことができる。2方向に分けて考えることと、時間tを経由して2種類の方向の運動をつなぐということを頭に入れておこう。

斜方投射

今度は斜め向きに初速度を与えたときの運動を考えよう。これを「斜方投射」という。斜方投射も水平方向と鉛直方向の運動に分けると考えやすい。
- 水平方向…等速直線運動
- 鉛直方向…鉛直投げ上げ

注意しなくてはならないのは、初速度が斜め向きだから、初速度も水平成分と鉛直成分に分けて考える必要があるということ。それぞれの方向の成分を使って、それぞれの方向の運動を考えよう。

では次の問題に挑戦しよう。初速度25m/sで斜め上向きにボールを投げ上げた。地面に落下した場所までの距離を求めよ。ただし、初速度の水平成分の大きさを15m/s,鉛直成分の大きさを20m/sとする。
まず、鉛直方向の運動(鉛直投げ上げ)に注目して、地面に落下するまでの時間tを求める。y=0として、

続いて水平方向の運動(等速直線運動)を考えて、水平方向の移動距離を求める。

