力の表し方
さあいよいよ力の話に入ろう。第1章では主に公式を使って答えを求めてきたが、これから学ぶ分野では、図が重要な武器になる。そこで今回は、そんな「図の描き方」を練習していこう。
力のはたらき

まず「力」とは何か。数式で表すのは後に回すとして、今は力がどのようなはたらきをするものなのかを考えてみたいと思う。力を加えると、バネや粘土のようなものは変形する。また、ボールを投げたり受けたりすることを考えれば、力によって物体の運動の状態が変化する。このことから、力を「物体を変形させたり、物体の運動の状態を変えたりする働きを持つもの」と考えておこう。
力の表し方
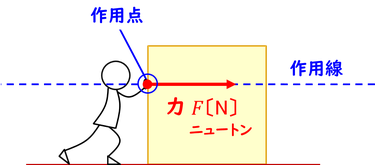
力は向きを持つ量だ。このことはとても大切。だから、向きであることを強調して、矢印で表そう。このときのポイントは、力がはたらく点(「力の作用点」という)と、力の向きに気を付けること。長さを変えることで、力の大小の表現も可能だ。また、力の矢印が乗っている直線を、「力の作用線」という。
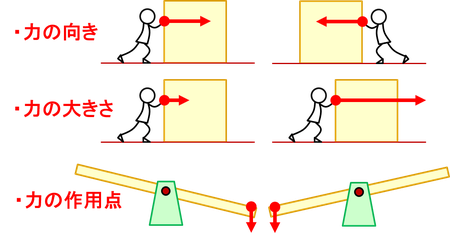
力の向きや、大きさや、作用点を変えると、その力のはたらきが変わる。このことから、力の向きと大きさと作用点を「力の三要素」と呼ぶ。作用点の違いによる力のはたらきの違いは、例えばシーソーを考えると分かりやすいのではないだろうか。右側を押せば右側が下がり、左側を押せば左側が下がる。
力の分類

重力や静電気力、磁気力などのように、離れた物体から受ける力がある。このような力を「遠隔力」という。これに対して、手が物体を押す力などの多くの力は、接触したほかの物体や人から受ける力である。このような力を「近接力」という。
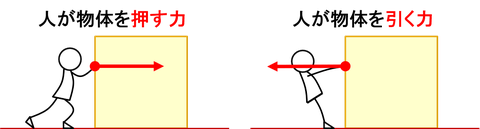
近接力は、「押す力」と「引く力」に分類できる。作用点は他の物体や人との接点であり、向きは図を見ても分かるように、押す力は注目物体の内部へ向かう向き、引く力は注目物体から離れる向きである。このように、押す力か引く力かに気を付けることで、力の向きを間違えずに書くことができる。

このことは、もちろん物体どうしの間ではたらく力にも言うことができる。例えば床が物体を「押す力」は注目物体の内部へ向かう向きだし、糸が物体を「引く力」は注目物体から離れる向きになっていることが分かるだろう。自分で書けそうかな?
作用反作用の法則

人や物を押すと、逆に押し返される力もはたらく。この2つの力は、例えば「人が物体を押す力」と「物体が人を押す力」と表現することができる。ここでこの力の説明をよく見てみると、【人】と【物体】が入れ替わっているだけであることに気付くことができる。このような関係の2つの力を、「作用・反作用」と呼ぶ。どちらが作用でどちらが反作用かは区別しないが、大切なことは、作用と反作用は必ずペアではたらくということ。力には、必ず
- 一直線上
- 同じ大きさ
- 逆向き

という関係式が成り立っている。

重力にも反作用がある。重力は「地球が物体を引く力」と言い換えることができるから、この反作用は「物体が地球を引く力」であることがわかる。物体が地球に引き寄せられているのと同時に、地球も物体に引き寄せられているのだ。

作用と反作用について、もう一つ言っておきたいことがある。それは、はたらいている物体が異なるということ。「人が【物体を】押す力」は物体にはたらく力であり、「物体が【人を】押す力」は人にはたらく力なのだ。このように、説明文の【〇〇を】に注目することで、その力がどの物体や人にはたらいている力なのか判断することができる。覚えておこう。

床の上に机を置き、机の上にリンゴを置く。このとき、りんごと机、机と床の間で及ぼし合う作用・反作用の矢印を書いてみた。それぞれ、どの物体にはたらいている力なのか、自分で判断ができるだろうか。
力のつり合い

机の上で静止しているりんごには、「重力」と「机がりんごを押す力」がはたらいている。このとき、この2力は
- 一直線上
- 逆向き
- 同じ大きさ

という関係が成り立っている。

静止している机には、「重力」と「りんごが机を押す力」と「床が机を押す力」という3つの力がはたらいている。机は静止しているから、りんごと同様に、机にはたらく力はつり合っているといえる。ただし、上向きの力が1つであるのに対し、下向きの力は2つだから、下向きの力は、”力を合わせて”上向きの力に対抗していることになる。だから、下向きの力の「和」が、上向きの力と等しくなっている。

少し分かりにくいかもしれないけれど、一般に物体が静止いているとき、上向きの力の「和」と、下向きの力の「和」が等しくなっている。同じ向きの力を足し合わせて考える必要があるということを覚えておこう。
最後に、作用反作用の復習。力F1~F5のうち、F2とF3は作用反作用の関係にあるから、

という関係も成り立っている。
