ミクロカノニカル分布
エネルギーE,体積V,分子数Nが一定の孤立系において、実現可能な微視的状態はどれも等確率で起こり得る。これを「等確率の原理」と呼んだ。もう少し話を進めてみよう。
エントロピー
前回、エネルギーが0~Eとなる微視的状態数を、
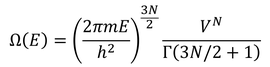
と表した。ガンマ関数は、mが1以上の整数のとき
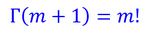
である。いまはNが非常に大きいので細かい数字は気にしないことにして、
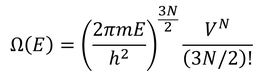
と書き換えよう。
続いて、エネルギーがE~E+ΔEの範囲になるときの微視的状態数を考えよう。これを、
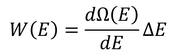
と決めてやる。計算すると、

となる。
これで、ボルツマンの関係式によって、エントロピーが計算できる。
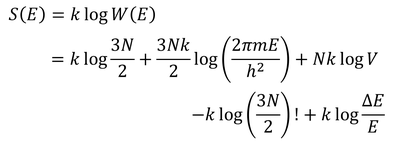
スターリグの公式(logN!≒NlogN-N)を使うと、
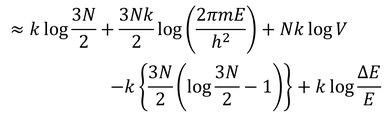
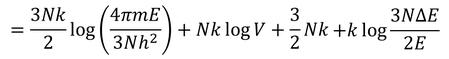
となる。最後の項はlogN程度、他の項はN程度の大きさなので、最後の項は無視することができる。

ギブスのパラドックス
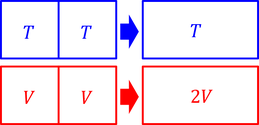
同じ温度の気体を接触させても、温度は変わらない。このような変数を「示強変数」という。圧力も示強変数である。これに対して同じ体積の気体を合わせるともちろん体積は2倍になる。このような変数を「示量変数」という。分子数やエントロピーは示量変数である。
エントロピーS(E,V,N)は示量変数なので、E,V,Nを2倍にするとエントロピーSも2倍にならなくてはいけない。ところが上の結果を眺めてみると、2倍にはならないのだ。これを「ギブスのパラドクス」という。
ここで、N個の分子がバラバラの状態になっているとき、その取り方が何通りあるか考えよう。1個目の分子の取り方はN通り、2個目の分子は(N-1)通り、3個目の分子は(N-2)通り…なので、合わせてN!通りの取り方がある。ただし、これはN個の分子に個性があって判別可能な場合だ。量子力学的にはこれらは判別不可能で、これらはすべて同じ状態ということになる。よって、
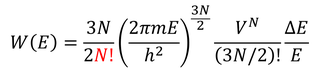
このように、前に求めた微視的状態数W(E)を重複していた数N!で割っておかなくてはならなかったのだ。すると、エントロピーは
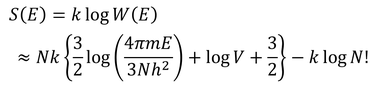
となり、最後の項はスターリングの公式によって
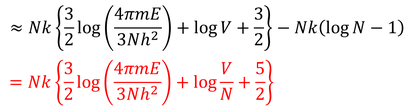
と書き変えられる。この結果であれば、E,V,Nを2倍にしたとき、エントロピーも2倍になっている。つまり示量変数になっている。
ミクロカノニカルアンサンブル
微視的状態数WからエントロピーSが得られたので、次はエントロピーから他の熱力学変数を求める方法を考えてみる。熱力学第1法則の微分形式
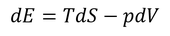
を思い出そう。この式は、内部エネルギーを増やすためにはエントロピーを増やしたり、体積を減らしたりする方法があることを示しているのだが、実は分子の数を増やしてもいい。そこで、この式へ次の項を加えよう。
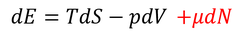
μは「化学ポテンシャル」と呼ばれる。ここで、左辺をdSとすると
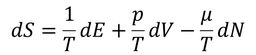
となるが、これを全微分の定義

と比較することで、

エントロピーを用いた3種類の関係式を得ることができる。この式から、温度Tや圧力p,化学ポテンシャルμが得られるのだ。
先に求めておいたエントロピーを用いて計算してみよう。1つめの関係式から
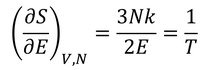
が得られ、この式から
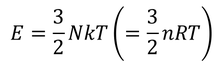
単原子分子理想気体の内部エネルギーを導くことができる。
2つめの関係式を用いると、
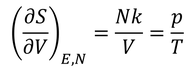
が得られるので、この式から
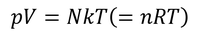
理想気体の状態方程式を導くことができる。

まとめよう。孤立系では、エネルギーE,体積V,分子数Nが決まった値のとき、あらゆる微視的状態は等確率で起こり得ると考えられるので、微視的状態数W(E,V,N)を使って、それぞれの確率は等しく

になっている。この確率分布を「ミクロカノニカル分布」と呼び、ミクロカノニカル分布で確率分布が表されるような系の集団を「ミクロカノニカルアンサンブル(小正準集団)」と呼ぶ。集団を考えることで、分子の統計的性質を詳しく調べることができるのだ。
ミクロカノニカルアンサンブルでは、まず微視的状態数Wを得ることが重要である。Wが得られれば、そこからエントロピー
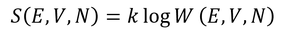
が得られ、エントロピーから
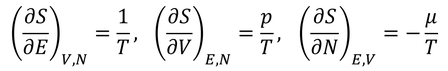
その他の熱力学変数を計算することができる。
