統計力学

グランドカノニカル分布 ←→ ボース分布

　ミクロカノニカル分布の話で、粒子の微視的状態数Wを考えるとき、粒子が区別できないものとしてN!で割ったのを覚えているだろうか。今回はこの量子的な効果について考えを深めていこう。

　容器内に区別のできない粒子が2つ入っているとしよう。このとき、波動関数が

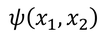
と表せるとする。ここで、粒子を入れ替えても存在確率が変わらないことから、

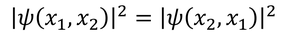
という関係が成り立ち、この式から

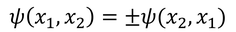
という2種類の関係が波動関数にはあることが分かる。

　入れ替えても波動関数が変わらない性質を持つ粒子を「ボース粒子（ボソン）」、波動関数の符号が反転する性質を持つ粒子を「フェルミ粒子（フェルミオン）」という。ボース粒子には光子、π中間子、ヘリウム原子などがある。フェルミ粒子には電子、陽子、中性子などがあり、フェルミ粒子を奇数個含む粒子もフェルミ粒子、フェルミ粒子を偶数個含む粒子はボース粒子である（例えば4,2ヘリウムはボース粒子、3,2ヘリウムはフェルミ粒子）。

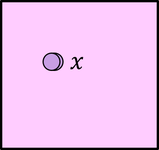
　ボース粒子が同じ位置にあるとき、上の波動関数の関係式は

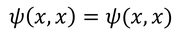
となるのに対し、フェルミ粒子の場合は

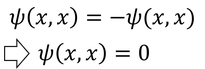
となる。これは、ボース粒子は同じ位置に複数の粒子が収まれるのに対し、フェルミ粒子は複数の粒子が収まることが許されないということを意味している。フェルミ粒子に関するこのきまりを「パウリの排他律（パウリの排他原理）」と呼ぶ。

　フェルミ粒子の性質を詳しく見ていこう。あるエネルギーの取り得る状態数が3個あり、その状態に2個の粒子が収まるパターンは上の3通りだ。これは、区別のできない2個の粒子と1個の空白部分の組み合わせなので、

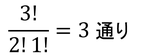
と計算できる。

　一般化しよう。Δ個の状態にn個の粒子を収めるパターンは、n個の区別できない粒子とΔ-n個の空白部分の組み合わせだから、

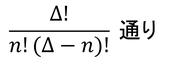
である。これをｊ番目のエネルギー状態における微視的状態数だとする。これをすべてのエネルギーだけ掛け合わせることで、全微視的状態数Wが得られる。

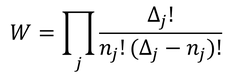
Π（総乗）は掛け合わせるという記号である。熱平衡時には微視的状態数Wが最大になることは以前にも見た。今回もWが最大になるようなn1,n2,…を探そう。まず、計算しやすいようにlogWを求める。

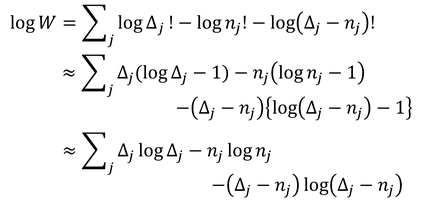
Δやnは1よりも十分に大きいとし、1行目から2行目はスターリングの公式（logN!≒NlogN-N）を使った。

　ミクロカノニカルアンサンブルの方法を考え、粒子数とエネルギーを一定とする。

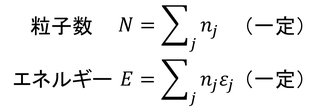
この条件の下でlogWを最大にするようなn1,n2,…を探す。そのためにはlogW,N,Eの変分

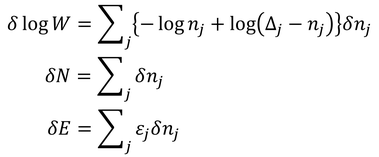
を考え、ラグランジュの未定乗数法を使う。

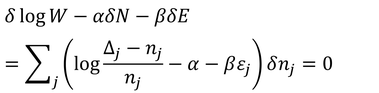
（　）の中身が0になるとき、njは

である。これは熱平衡時のエネルギーεjごとの粒子の数を示す。この確率分布を「フェルミ分布（フェルミ・ディラック分布）」という。また、状態数Δjで割ることで、

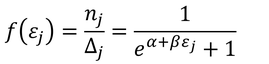
状態ごとの確率分布を得ることができる。

　あとは定数α,βを決めなければならない。そのためにはボルツマンの関係式（S=klogW）を使ってエントロピーを求め、

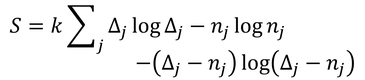
熱力学から得られる以下の関係式を使う。

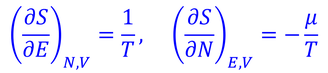
　エントロピーをエネルギーで偏微分することで

βが得られる。

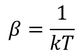
　続いてエントロピーを粒子数で偏微分して

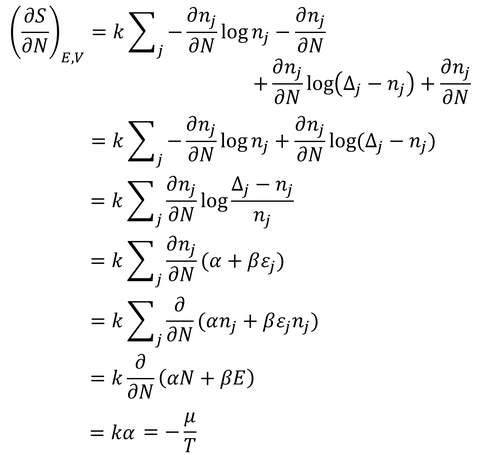
αが得られる。

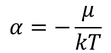
こうして、

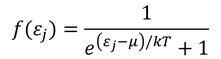
エネルギーごとの確率分布が得られる。

　フェルミ粒子の例として金属内の電子を考える。エネルギーは連続であるとして、確率分布を

と表す。これを「フェルミ分布関数」と呼ぶ。

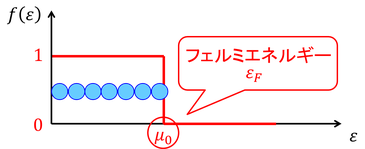
　絶対零度（T=0）のときのフェルミ分布関数は上図のようになる。粒子は低いエネルギー状態から順番に収まっていくが、1つの状態には1つの粒子しか収まることができないため、あるエネルギーμ0よりも低いエネルギーで粒子は1つずつ収まっていることになる。絶対零度における化学ポテンシャルμ0を「フェルミエネルギー」といい、εFと表される。

　温度が0よりも大きな場合のフェルミ分布関数は上図のようになる。化学ポテンシャルμ付近の粒子は上のエネルギーに粒子がいないため、わずかに飛び出すことができるのだ。

　フェルミエネルギーεFを求めてみよう。まず、電子が取り得る状態数Ωを考える。フェルミエネルギーεFに対応する運動量pFを考えて、

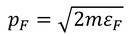
これを「フェルミ運動量」と呼ぶことにする。すると、エネルギー0～εFを持つ電子は運動量0～pFを持つと考えられるから、これらの電子は、運動量空間で半径pFの球の体積I内に存在することになる。その体積は

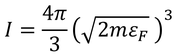
である。状態数Ωは位相空間での体積VIをプランク定数ｈの3乗で割ることで得られる。

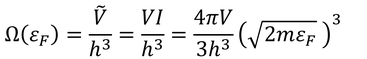
ここでT=0のフェルミ分布によると、εFまでの粒子は取り得る状態にきちんと収まっているわけだから、状態数Ωは粒子数Nと一致していることが分かる。

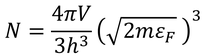
ただし、電子にはスピンという性質があり、上向きスピン・下向きスピンという2種類の状態を取ることができる。別のスピンを持つ2つの電子は1つの状態に収まることができるため、いま求めた粒子数の2倍の電子が存在できるのだ。

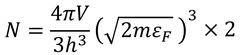
電子の数Nが分かっているとすれば、この式からフェルミエネルギーεFが得られる。

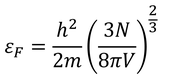
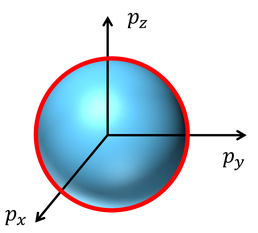
　ところで、いま考えた運動量空間における半径pFの球を「フェルミ球」、その表面を「フェルミ面」と呼ぶ。このように、温度が低いときには低いエネルギー状態から順番にフェルミ粒子は収まっていく。このような現象を「フェルミ凝縮」と呼び、フェルミ粒子が量子的な効果を得てフェルミ凝縮を起こすようになる温度を「フェルミ温度」という。フェルミ温度TFは次のように定義できる。

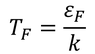
銅、ナトリウム、カリウム1molが1molの自由電子を放出しているとすれば、フェルミ温度は上の式から

• 銅…81000K
• ナトリウム…37000K
• カリウム…24000K

となる。このことから、室温程度であれば電子がフェルミ凝縮するには十分低温であることが分かる。