カノニカル分布
前回は「ミクロカノニカルアンサンブル」という統計集団を考えた。微視的状態数W(E,V,N)からエントロピーS(E,V,N)が得られ、エントロピーから他の熱力学変数が求められるのだった。今回は前回とは異なる統計集団を紹介しよう。
カノニカルアンサンブル
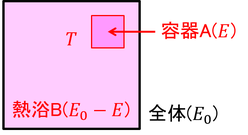
前回考えた孤立系の内部の領域Aに注目する。このAの体積はVで含まれる分子数はNであるとしよう。前回と異なるのは、外部とエネルギーをやりとりするという点だ。この領域を容器A,外部を熱浴Bと呼ぼう。容器Aは熱浴Bとエネルギーをやり取りして、両者の温度はTに保たれているとする。ただし、全体のエネルギーE0は孤立系なので変わらない。このとき、容器AのエネルギーがEになる確率P(E)は、熱浴Bのエネルギーが(E0-E)となる確率と等しいから、A,B,全体の微視的状態数W,WB,W0を使って、

と表すことができる。
ここで、ボルツマンの関係式より熱浴BのエントロピーS_Bは

となるから、逆に微視的状態数W_BをエントロピーS_Bで表すこともできる。
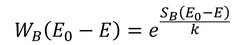
また、E_0>>Eとすると、エントロピーS_Bは、
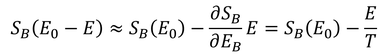
と書けるから、
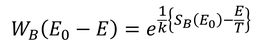
となる。これを確率P(E)の式へ適用することで、

を得る。e^(-E/kT)はボルツマン分布のときにも登場したのを覚えているだろうか。この部分を「ボルツマン因子」という。
では、容器AのエネルギーがEとなる微視的状態のうち、1つの状態Enに注目してみよう。
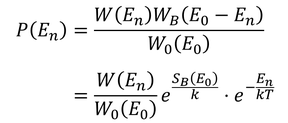
縮退していなければW(En)=1である。また、W0とS_B(E0)は定数だから、この式は

と簡単に書くことができる。Zは定数であり、エネルギーがEとなる場合の微視的状態数だけ足し合わせると確率が1になるという規格化条件によって
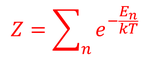
と決まる。これを「分配関数」と呼ぶ。

確率分布が上記のように表される分布を「カノニカル分布」と呼び、このような系を集めた集団を「カノニカルアンサンブル(正準集団)」と呼ぶ。
自由エネルギー

分子の統計的性質を調べる際、ミクロカノニカルアンサンブルでは微視的状態数Wからエントロピーを求め、その他の熱力学変数を計算した。カノニカルアンサンブルでは微視的状態数Wの代わりに分配関数Zを用い、エントロピーの代わりに自由エネルギーを求めることで、その他の熱力学変数が得られる。
熱力学で定義される(ヘルムホルツの)自由エネルギーは
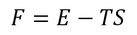
であった。Eは内部エネルギーである。
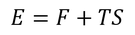
ここで、自由エネルギーFをTで偏微分すると

だから、これをEの式へ代入して、

を得る。
続いて、カノニカル分布から内部エネルギーを考えてみよう。エネルギーEnの平均値<E>を考えるわけだ。確率とエネルギーの積をすべての状態の数だけ足し合わせればいいから、
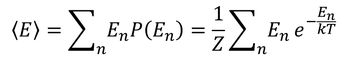
である。ここで、logZをTで偏微分すると
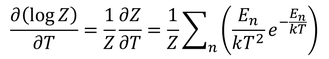
となるが、この式は<E>を用いて

と表すこともできる。よって、
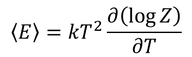
を得る。この結果を、自由エネルギーFを用いた内部エネルギーEの式と比較することで、

分配関数Zと自由エネルギーFの関係式が得られる。ボルツマンの関係式「S=klogW」と似ている。
また、自由エネルギーの熱力学的な定義式F=E-TSの微分
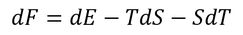
に熱力学第1法則の微分形式を代入してまとめると

となるから、全微分

と比較をすることで、

自由エネルギーFを用いた3種類の関係式が得られる。このように、カノニカルアンサンブルでは、分配関数Zから自由エネルギーFを求めることで、そのほかの変数が計算できるのだ。
理想気体への適用

では具体的に考えてみよう。分子1個の運動エネルギーが

だから、内部エネルギーEは
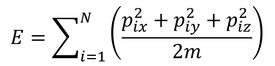
となる。これを用いて分配関数Z(E,V,N)を求める。分配関数を求める際に微視的状態数が必要になるが、これは『等確率の原理』のページで説明したように位相空間の体積をN!とh^(3N)で割ることで得られるから、

と表せる。pは分子1個あたり3成分あることに注意して計算すると

となる。式変形にはガウス積分

を用いた。
では、この分配関数Zを用いて自由エネルギーFを求めよう。ZとFの関係式を使って、
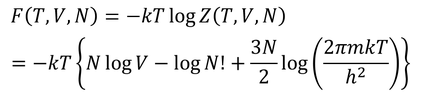
となる。logN!にはスターリングの公式(logN!≒NlogN-N)が使えるから
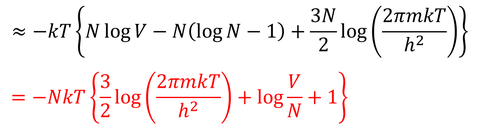
を得る。
この自由エネルギーFを用いることで、他の熱力学変数を計算することができる。まずエントロピーSは、

となる。続いて圧力pも
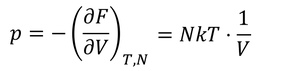
と計算できる。この式は、

理想気体の状態方程式である。
ほかには、内部エネルギーEと求めることもできる。

